cos5x>1/2 trygonometria trygo:

	1
cos5x>		dla −π≤x≤π
	2

Robię to tak 5x=t

	1		π		π
rysuję cost i sprawdzam kiedy cost>		wychodzi mi ze dla t∊(−		;		)
	2		3		3

	π		π
teraz pod t podstawiam 5x i piszę że x∊(−		;		)
	15		15

Tylko, że tych rozwiązań mieści się w przedziale więcej, jak je znaleźć?

	π		π
Powinienem zapisać to jako (−		+2kπ;		+2kπ)?
	3		3

J:

	π		π
−		+ 2kπ lub		+ 2kπ
	15		15

Janek191:

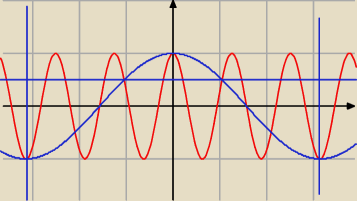
PW: Taki jest częsty błąd: zapominamy, że jeśli x∊<−π, π> to 5x∊<−5π, 5π>. Twoje t należy więc do 5 razy dłuższego przedziału.

trygo: czyli rozwiazac mozna na pare sposobow, albo zwiekszyc przedzial albo zapisac w postaci +2kπ i szukać wszystkich rozwiazan podstawiajac pod k kolejne liczby całkowite, dzieki