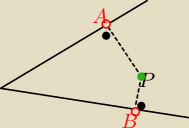
Kąt ostry Przemysław: Punkt P leży wewnątrz kąta ostrego. Na ramionach tego kąta wyznacz takie punkty A i B, dla których obwód trójkąta ABP jest najmniejszy. Próbowałem tak, jak na rysunku: Żeby odcinek AP był najkrótszy to musi leżeć na prostej prostopadłej do ramienia, przechodzącej przez P; analogicznie dla BP. Niestety to nie mówi nic o długości AB. Ale nie wiem, czy ta odpowiedź jest dobra, ani jak sprawdzić czy jest dobra... Proszę o pomoc

Kacper: Skąd takie zadanie?

Przemysław: Oj tam, wszystko musisz wiedzieć

Kacper: No muszę, bo wygląda na zadanko z jakiegoś konkursu

Kacper: wsk. pomyśl nad pewnymi symetriami

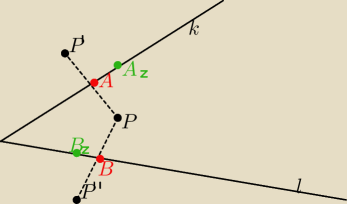
Przemysław: https://www.omg.edu.pl/uploads/attachments/kwadrat_02-czerwony.pdf Nadrabiam zaległości z gimnazjum Dobra, spojrzałem do gazetki i chyba mam rację: Niech ramię z punktem A leży na prostej k, ramię z punktem B leży na prostej l. P' to odbicie P względem k, P'' to odbicie P względem l. Teraz A to punkt przecięcia PP' z k, B to punkt przecięcia PP'' z l. By udowodnić, że to szukane punkty weźmy: A₂, leżące na k, B₂, leżące na l. Trzeba udowodnić, że A₂P+B₂P+B₂A₂≥AP+BP+AB Z nierówności trójkąta: 1^o P'A₂+A₂P≥P'A+AP 2^o P''B₂+B₂P≥P''B+BP Z symetrii osiowej: A₂P=A₂P' B₂P=B₂P'' AP=AP' BP=BP'' Więc mamy pokazać, że: A₂P'+B₂P''+B₂A₂≥P'A+P''B+AB Dodajmy 1^o i 2^o stronami: P'A₂+A₂P+P''B₂+B₂P≥P'A+AP+P''B+BP Pozostaje nam więc pokazać, że: A₂P+B₂P≥AP+BP ⇒B₂A₂≥AB Mamy zaś: BP+AP≥AB czyli: A₂P+B₂P≥AP+BP ⇒A₂P+B₂P≥AB Pozostaje tylko: A₂P+B₂P≤B₂A₂ Mamy jednak z nierówności trójkąta: A₂P+B₂P≥B₂A₂ więc jedyna możliwość to A₂P+B₂P=B₂A₂ Czyli chyba coś namieszałem?

Kacper: Strasznie długie rozważania Moje pytanie: Twierdzisz, że punkty A i B to szukane punkty? To muszę cię rozczarować i powiedzieć nie

Przemysław: Czemu?

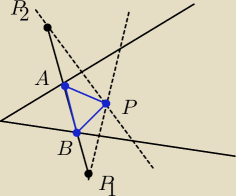
Kacper: Bo da się znaleźć trójkąt o mniejszym obwodzie Trójkąt APB jest tym o najmniejszym obwodzie Teraz trzeba tylko "ładne" uzasadnienie podać

Przemysław: No nie wiem Umiesz to uzasadnić? Bo wskazówka do zadania: "Odbij punkt P symetrycznie względem ramion kąta, a następnie połącz odcinkiem tak otrzymane punkty. Punkty przecięcia tego odcinka z ramionami kąta są szukanymi punktami A i B. Aby wykazać, że tak skonstruowane punkty stanowią rozwią− zania zadania, wybierz dwa dowolne punkty A i B na ramionach tego kąta i uzasadnij, że obwód trójkąta ABP jest większy lub równy od obwodu trójkąta ABP." Co sugeruje, że to nie są te punkty, o których piszesz (możliwe, że jest błąd w tej gazetce, ale nie sądzę).

Przemysław: Niestety muszę iść Jak by co to napisz, co o tym sądzisz jeśli możesz a ja potem przeczytam. Dziękuję bardzo za zajęcie się moim problemem

Kacper: Przecież ja dokładnie zrobiłem, to co ty napisałeś Odbiłem symetrycznie punkt P względem ramion kąta (punkty P₁ i P₂) Następnie łącze te punkty (Odcinek P₁P₂). Punkty przecięcia odcinka i ramion to nasze punkty A i B

Przemysław: Ależ ja nie myślę... To jest żałosne wręcz No nic i tak bywa. Wygląda na to, że czytanie to pożyteczna umiejętność. Dziękuję bardzo za pomoc. Jak dam radę, to postaram się potem jeszcze to uzasadnić.

Przemysław: Dobrze. Wydaje się, że uzasadnienie jest "ładne" i proste: Oznaczenia: A' − dowolny punkt na ramieniu kąta zawierającym A B' − dowolny punkt na ramieniu kąta zawierającym B Twierdzę: A'P+B'P+A'B'≥AP+PB+AB Zauważmy: (z symetrii osiowej):

⎧	(1) A'P=A'P2
⎜	(2) B'P=B'P1
⎨	(3) AP=AP2
⎩	(4) BP=BP1

(z nierówności trójkąta): P₂A'+A'B'+P₁B'≥P₁P₂=P₂A+AB+P₁B=AP+AB+BP (z (3) i (4) ) Otrzymaliśmy: P₂A'+A'B'+P₁B'≥AP+AB+BP Stosujemy (1) i (2): PA'+A'B'+PB'≥AP+AB+BP Co jest równoważne z Twierdzeniem, więc wykazaliśmy, że obwód trójkąta A'B'P jest zawsze niemniejszy od obwodu trójkąta ABP (równość zachodzi tylko dla A'=A, B'=B). Mam nadzieję, że nie narobiłem znowu głupot.