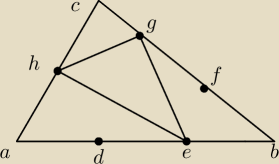
W trójkącie ABC punkty D, E dzielą bok
AB na trzy odcinki równej długości; punkty F,
G dzielą bok BC na trzy odcinki równej długości,
a punkt H jest środkiem boku AC (zobacz
rysunek obok). Wykaż, że pole trójkąta EGH
stanowi 5/18 pola trójkąta ABC.
Proszę o pomoc i wytłumaczenie 
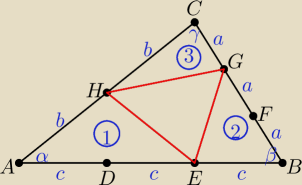
| 1 | ||
Pole trójkąta ABC = P = | *2b*3c*sinα = 3bcsinα | |
| 2 |
| 1 | 9 | |||
Pole trójkąta ABC = P = | *3a*3c*sinβ = | acsinβ | ||
| 2 | 2 |
| 1 | ||
Pole trójkąta ABC = P = | *2b*3a*sinγ = 3absinγ | |
| 2 |
| 1 | 1 | |||
Pole trójkąta (1) P1 = | b*2c*sinα = bcsinα = | P | ||
| 2 | 3 |
| 1 | 2 | |||
Pole trójkąta (2) P2 = | c*2a*sinβ = acsinβ = | P | ||
| 2 | 9 |
| 1 | 1 | |||
Pole trójkąta (3) P3 = | a*b*sinγ = | P | ||
| 2 | 6 |
| 1 | 2 | 1 | ||||
P1 + P2 + P3 = | P + | P + | P = ... ⇒ ... dokończ | |||
| 3 | 9 | 6 |
mam tylko jeszcze pytanko : co się dzieje z sin np. w tym polu trójkąta (1) ?
| P1 | bc sinα | 1 | 1 | |||||
np. | = | = | ⇒ P1 = | P | ||||
| P | 3bc sinα | 3 | 3 |
