maturalne zadanie optymalizacyjne YushokU: Witam, Mam kłopot z zadaniem. Nie za bardzo wiem jak je dokończyć. Dana jest parabola o równaniu f(x)=−x2+4x. Oblicz współrzędne takiego punktu P należącego do tej paraboli, że styczna do paraboli poprowadzona w punkcie P wraz z prostymi o równaniach: x=0, x=2, y=0 wyznaczają trapez o najmniejszym polu. Moje rozwiązanie: f'(a)=−2a+4 f'(a)=−a²+4a Styczna ma postać. y=(−2a+4)x+b a∊(0,2) Jest styczna do f(x) w punkcie a. −a²+4a=−2a²+4a+b b=a² y=(−2a+4)x+a² Oznaczam punkt A(2,0), D(0,0) B(2,y) y=−4a+8+a²=a²−4a+8 B(2,a²−4a+8) C(x,0) 0=−(2a−4)x+a² a≠0 x=U{a²}{2a−4) Czyli wzór na pole ma postać.

	a2
P(a)=0,5*(AB+CD)*BD=(AB+CD)=a2−4a+8+
	2a−4

No dobra, na razie wszystko pięknie, ale pochodna wygląda tak:

	a2−4a		4a3−23a2+44a−32
P'(a)=2a−4+		=
	2(a−2)		2(a−2)2

Ktoś widzi jakiś błąd, jakieś uproszczenie? Odpowiedź jest dla a=1 .Z góry dzięki, bo wiem, że przed maturami to macie kupe roboty z nami−maturzystami

YushokU: Dobra, stwierdziłem, że porównam tą funkcję nieułamkową. Zawsze lubiłem mieć wszystko w jednym ułamku, ale nie tym razem

	10−2√5
Ale nadal nie ten wynik co potrzeba, bo dla a=		. Ktoś sprawdzi?
	5

PW: Jeżeli styczna ma równanie y = (−2a+4)x + a², to przecina oś OY w punkcie C o współrzędnych (0, a²). Ty policzyłeś, kiedy y = 0, czyli odciętą punktu, w którym styczna przecina oś OX − ten punkt nie jest potrzebny do rozwiązania (nie jest punktem C).

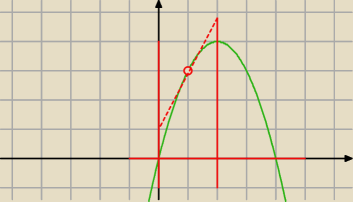
===: ... zawsze rysunek ! ... zawsze myślenie ! i nie rzucaj się na zadanie jak szczerbaty na suchary − cosik świta? −

YushokU: Nie no, wszystko miałem narysowane, ale sobie źle oznaczyłem punkt. Wychodzi, dzięki, bo samemu to ciężko czasem zauważyć Pierwszy oznaczyłem dobrze, drugi źle. Czemu? Nie wiem.