trapez
zadanq: W trapezie ABCD ramiona mają długości 6 i 8, a odcinek łączący środki przekątnych ma długość 5.
Obliczyć odległość między środkami podstaw tego trapezu.
a−b=10 ⇒ a= 10+b
co dalej?
4 maj 20:51
zadanq: hm
4 maj 21:12
Janek191:
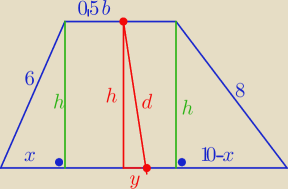
Mamy
| a − b | |
| = 5 ⇒ a − b = 10 ⇒ a = b + 10 |
| 2 | |
oraz
h
2 − 6
2 − x
2 = 36 − x
2
h
2 = 8
2 − ( 10 − x)
2 = 64 − 100 + 20 x − x
2
więc
36 − x
2 = − 36 + 20 x − x
2
72 = 20 x
x = 3,6
=====
10 − x = 6,4
========
h
2 = 36 − 3,6
2 = 36 − 12,96 = 23,04
h = 4,8
======
y = 0,5*( b + 10) − ( x + 0,5 b) = 0,5 b + 5 − 3,6 − 0,5 b = 1,4
y = 1,4
======
d
2 = h
2 + y
2 = 23,04 + 1,96 = 25
wiec
d = 5
=====
4 maj 21:29
Janek191:

Mamy
| a − b | |
| = 5 ⇒ a − b = 10 ⇒ a = b + 10 |
| 2 | |
oraz
h
2 − 6
2 − x
2 = 36 − x
2
h
2 = 8
2 − ( 10 − x)
2 = 64 − 100 + 20 x − x
2
więc
36 − x
2 = − 36 + 20 x − x
2
72 = 20 x
x = 3,6
=====
10 − x = 6,4
========
h
2 = 36 − 3,6
2 = 36 − 12,96 = 23,04
h = 4,8
======
y = 0,5*( b + 10) − ( x + 0,5 b) = 0,5 b + 5 − 3,6 − 0,5 b = 1,4
y = 1,4
======
d
2 = h
2 + y
2 = 23,04 + 1,96 = 25
wiec
d = 5
=====
4 maj 21:30
Janek191:
Pod oraz powinno być
h2 = 62 − x2 = 36 − x2
4 maj 21:31
Bogdan:
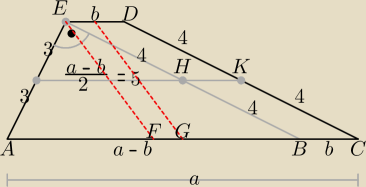
Prawie bez obliczeń (szkic rozwiązania)
|AC| = a, |DE| = b, |AB| = a − b,
| | a−b | | a−b | |
Odległość między środkami przekątnych jest równa |
| , tu |
| = 5 ⇒ a − b = 10 |
| | 2 | | 2 | |
Trójkąt ABE jest prostokątny (6
2 + 8
2 = 10
2), przeciwprostokątna AB ma długość 10,
szukana odległość między środkami podstaw jest równa długości środkowej tego trójkąta.
Długość środkowej trójkąta prostokątnego jest równa długości promienia R okręgu
| | 1 | |
opisanego na takim trójkącie. W tym przypadku R = |
| *|AB| = 5 |
| | 2 | |
4 maj 22:01
 Mamy
Mamy
 Mamy
Mamy
 Prawie bez obliczeń (szkic rozwiązania)
|AC| = a, |DE| = b, |AB| = a − b,
Prawie bez obliczeń (szkic rozwiązania)
|AC| = a, |DE| = b, |AB| = a − b,