... Phoebe Campbell:

	4
Mam funkcję wymierną f(x) =		.
	x

Mam za zadanie określić m.in. przedziały monotoniczności (co potrafię) oraz określić czy funkcja jest monotoniczna w zbiorze R\{0}. Tego niestety już nie potrafię zrobić. Proszę więc o wytłumaczenie. Dzięki

b.: I sposób Na półprostych (−∞,0) oraz na (0,∞) f jest malejąca. Trzeba więc porównać granice jednostronne w zerze −− jeśli lewostronna jest większa równa od prawostronnej, to f jest malejąca na R\{0}. II sposób f(1) > f(2), ale f(−1) < f(1), więc f nie jest monotoniczna na R\{0}.

Kacper: Wolę sposób II

Phoebe Campbell: Drugi sposób wygląda lepiej, ale.. nie rozumiem go. Możesz opisać to słowami?

b.: Żeby pokazać, że f nie jest monotoniczna, wystarczy pokazać, że nie jest ani rosnąca, ani malejąca, i to robię na 2 przykładach

Janek191:

	4
f(x) =
	x

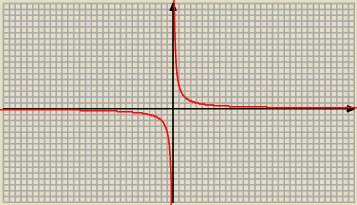
f nie jest monotoniczna na ℛ \ { 0} bo np. − 1 < 1 , a f( − 1) < f(1)

Karka: Czy do wykresu funkcji nierosnącej mogą należeć punkty: a) A (−4,2), B (−1,2), C(1,1), D (2, −3 ) E (5,−3) ?

J: tak

Karka: mógłbyś mi to jakoś wytłumaczyć ?

J: ze wzrostem argumentu, wartość funkcji nie rośnie , a tak jest dla funkcji rosnącej

Karka: ok ,dzięki

Karka: naszkicuj wykres funkcji f. Czy jest to funkcja monotoniczna ?

	1
a) ⎧−		x+2 dla x<0
	2

f(x) = ⎨ ⎩ 2 dla x≥0

J: zaóż nowy temat

Karka: nie wiem jaaak .. ;c

J: kliknij u góry na: dodaj nowe zadanie

Karka: ok

Karka: juuz