prawdopodobienstwo dispi:

	1		1
Oblicz P(A'∩B) jeśli P(A')=		oraz P(A'∩B')=
	4		7

	3
wiem że P(A)=
	4

	6
P(A∩B)=
	7

P(A−B)=P(A∩B')=P(A)−P(A∩B) ale z tego wychodzi mi ujemne

PW: Niestety, tu jest błąd: dopełnieniem zbioru A'∩B' jest zbiór A∪B, a nie jak sądzisz A∩B (wzory de Morgana).

Mila: (A'∩B')'=A∪B

dispi:

	6
czyli P(A∪B)=		tak
	7

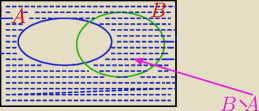
Mila: Tak. A'∩B=B\A P(A∪B)=P(A)+P(B)−P(A∩B)

6		3
	=		+(P(B)−P(A∩B))⇔
7		4

6		3
	−		=P(B\A)
7		4

Teraz dokończ