Potrójna wartość bezwzględna pomocy
Paul: |||x−1|−1|−1 ≤ 1
Jak to rozwiązać?
3 maj 22:29
Godzio:
Algebraicznie czy graficznie (to drugie chyba szybsze)?
3 maj 22:29
Paul: Najlepiej oba sposoby żebym dokładnie to zrozumiał.
3 maj 22:31
Godzio:
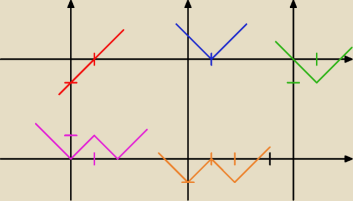
|||x − 1| − 1| − 1| ≤ 1
||x − 1| − 1| − 1 ≤ 1 i ||x − 1| − 1| − 1 ≥ − 1
||x − 1| − 1| ≤ 2 i ||x − 1| − 1| ≥ 0 −− druga nierówność zawsze prawdziwa, pomijam.
|x − 1| − 1 ≤ 2 i |x − 1| − 1 ≥ − 2
|x − 1| ≤ 3 i |x − 1| ≥ − 1 −− druga nierówność zawsze prawdziwa, pomijam
x − 1 ≤ 3 i x − 1 ≥ − 3
x ≤ 4 i x ≥ −2
x ∊ <−2,4>
3 maj 22:39
Godzio:
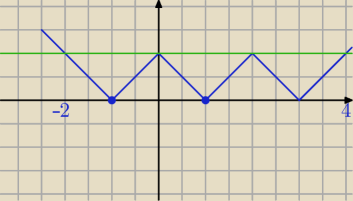
f(x) ≤ 1 dla x ∊ <−2,4>
3 maj 22:39
Godzio: Wykresy przedstawiają kolejne obniżenia i nakładanie wartości bezwzględnych:
x − 1 → |x − 1| → |x − 1| − 1 → ||x−1|−1|→ ||x−1|−1|−1→|||x−1|−1|−1|
3 maj 22:40
Paul: Dziękuję bardzo!
3 maj 22:41
 |||x − 1| − 1| − 1| ≤ 1
||x − 1| − 1| − 1 ≤ 1 i ||x − 1| − 1| − 1 ≥ − 1
||x − 1| − 1| ≤ 2 i ||x − 1| − 1| ≥ 0 −− druga nierówność zawsze prawdziwa, pomijam.
|x − 1| − 1 ≤ 2 i |x − 1| − 1 ≥ − 2
|x − 1| ≤ 3 i |x − 1| ≥ − 1 −− druga nierówność zawsze prawdziwa, pomijam
x − 1 ≤ 3 i x − 1 ≥ − 3
x ≤ 4 i x ≥ −2
x ∊ <−2,4>
|||x − 1| − 1| − 1| ≤ 1
||x − 1| − 1| − 1 ≤ 1 i ||x − 1| − 1| − 1 ≥ − 1
||x − 1| − 1| ≤ 2 i ||x − 1| − 1| ≥ 0 −− druga nierówność zawsze prawdziwa, pomijam.
|x − 1| − 1 ≤ 2 i |x − 1| − 1 ≥ − 2
|x − 1| ≤ 3 i |x − 1| ≥ − 1 −− druga nierówność zawsze prawdziwa, pomijam
x − 1 ≤ 3 i x − 1 ≥ − 3
x ≤ 4 i x ≥ −2
x ∊ <−2,4>
 f(x) ≤ 1 dla x ∊ <−2,4>
f(x) ≤ 1 dla x ∊ <−2,4>