(A∩B)÷(A∩C)=A∩(B÷C) ledzeppelin20: Witam ,czy pomoże mi ktoś to udowodnić , z góry dziękuje za pomoc : (A∩B)÷(A∩C)=A∩(B÷C) Najlepiej by było jakby z lewej strony dojść do prawej lub na odwrót , bardzo proszę o pomoc i jeszcze raz z góry dziękuje za nią

nodi: Pisząc znak ÷ miałeś zapewne na myśli odejmowanie (strona 1059) zbiorów. (A n B) \ (A n C) = A n (B \ C) Korzystam z własności działań na zbiorach na stronie 1060. L = (A n B) \ (A n C) = (A n B) n (A n C)' = (A n B) n (A' u C') = = [(A n B) n A'] u [(A n B) n C'] = [A' n (A n B)] u [A n (B n C')] = = [(A' n A) n B] u [A n (B \ C)] = [∅ n B] u [A n (B \ C)] = = ∅ u [A n (B \ C)] = A n (B \ C) = P L = P c. n. u.

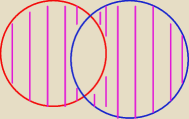
Janek191: To jest różnica symetryczna zbiorów A − B = ( A ∪ B ) \ ( A ∩ B )

ledzeppelin20: a to nie trzeba rozpisać, że x do czegoś należy itd. ?