http://www.pi.edu.pl/pliki/czemcke/Planimetria.pdf pilne
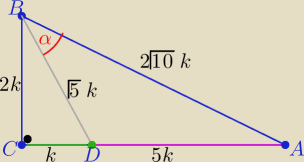Długości policzyłam z tw. Pitagorasa
z tw. kosinusów w ΔDAB:
| 5k2+40k2−25k2 | √2 | |||
cosα= | = ..........= | |||
| 2*√5k*2√10k | 2 |
Ja życzę powodzenia 
teraz robie jeszcze zadania z cke
x− wspólna miara, x>0
|BD|2=x2+4x2=5x2
|BD|=x*√5
c2=(2x)2+(6x)2=40x2
c=x*√40
| 1 | ||
PΔBDA= | *|BD|*c*sinα | |
| 2 |
| 1 | 2x | 2*√40 | √10 | |||||
PΔBDA= | *5x*c*sinδ, sinδ= | = | = | |||||
| 2 | x√40 | 40 | 10 |
| 1 | 1 | √10 | |||
*|BD|*c*sinα= | *5x*c* | ||||
| 2 | 2 | 10 |
| √10 | ||
x√5*sinα=5x* | ||
| 10 |
| √10 | ||
√5*sinα= | ||
| 2 |
| √2 | ||
sinα= | i α− kąt ostry⇔α=45o | |
| 2 |