Katy Ligia22: Punkty A, B, C lezą na okręgu o środku S (zobacz rysunek). Miara kata L jest równa? W środku okręgu zaznaczony jest punkt S który jest wierzchołkiem czworokąta i przy nim jest kat L i naprzeciwko niego.

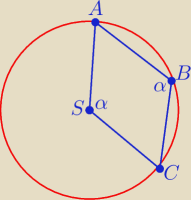
Janek191: α = 120^o

Ligia22: Dlaczego?

Kacper: Ja stawiam na α=135^o

Ligia22: Janek ma racje 😛 ale czemu?

Kacper: Ja też mam rację, bo sobie narysuje inny czworokąt i będzie po mojemu

Ligia22: Super, przydałoby sie wytłumaczenie tego 😁 Janek odezwij sie.

Kacper: Czy ty nie rozumiesz, że bez rysunku to każdy wynik jest możliwy?

Ligia22: Rysunek Janka jest poprawny.

Kacper: Janek jesteś jasnowidzem? Jeśli ten czworokąt jest rombem, to wystarczy dorysować jeden promień i mamy dwa trójkąty równoboczne. Stąd ten wynik

Ligia22: Nie, to zadanie ma rysunek i odpowiedz, taka jak u Janka 😉

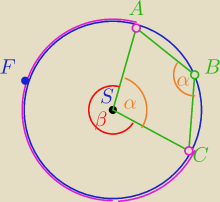
Mila: 1) ∡ASC=α− kąt środkowy oparty na łuku ABC 2) ∡ASC=β− kąt środkowy oparty na łuku AFC 3)α+β=360

	1
4) ∡ABC=α− kąt wpisany oparty na łuku AFC⇔α=		β
	2

	1		1
5) z (3)		β+β=360o⇔β=240o⇒α=		*240=120o
	2		2

PW: 292341 − musi być 120°.