matura Kacper: Proste zadanko Dany jest trójkąt prostokątny ABC, w którym przyprostokątne AB i AC mają odpowiednio długość a i a√2. W trójkącie poprowadzono środkową CD i wysokość AE. Wykaż, że punkt ich przecięcia jest środkiem okręgu opisanego na trójkącie ADC

misiek: Kacper czy na pewno dobrze podałeś treść zadania?

Kacper: To zadanie jest mi potrzebne do innego, zatem nie jest z książek Wiem, jak to pokazać, ale może ktoś wskaże łatwiejszy sposób

misiek: Nie odpowiedziałeś na moje pytanie: czy dobra jest treść!

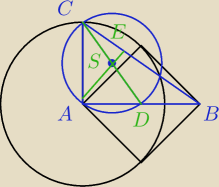
Kacper: Powinno być: AB i AC mają odpowiednio długość a√2 i a. Dołączam rysunek.

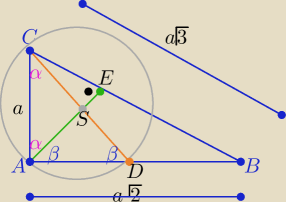
Eta: Hej Kacper |AC|=a, |AB|=a√2, |BC|=a√3

	a√6
Z Pitagorasa |DC|=
	2

	a*a√2		a√6
i |AE|=		=
	a√3		3

	√3		√6		√3
w ΔADC sinα=		i w ΔAEC cosα=		⇒ sinα=
	3		3		3

zatem trójkąty ASC i ADS są równoramienne o ramionach |AS|=|CS|=|DS|= R ............

Eta: Pasuje?

Kacper: Pasuje Eta Moje rozwiązanie też mniej więcej jest takiej długości. Zatem chyba nie da ominąć się kilku rachunków

Bogdan:

|AC|		|AD|
	=
|AB|		|AC|

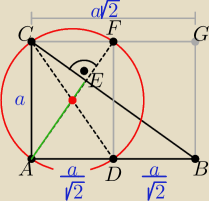
Można spróbować skorzystać z podobieństwa prostokątów ABGC i ADFC i z faktu, że przekątne AF i CD prostokąta ADFC przecinają się w punkcie będącym środkiem okręgu opisanego na tym prostokącie, a także na trójkącie ADC. Trzeba jeszcze uzasadnić, że przekątna AF zawiera wysokość AE trójkąta ABC.

nudammmmmmm: αγβΔ

nudammmmmmm: nigdy tego nie wkuję!