Trójkąt P: Dany jest trójkąt ostrokątny ABC o bokach długości a,b,c i kątach α,β,γ, przy czym a jest

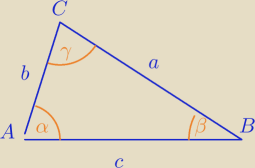
	a2+b2−c2
naprzeciw α, b − naprzeciw β, a c − naprzeciw γ. Wykaż, że		=tgα⋅ctgγ.
	b2+c2−a2

	sin2α+sin2β−sin2γ
Wyszło mi z twierdzenia sinusów :		. Co
	sin2β+sin2γ−sin2α

dalej?

Kacper: Przekształcaj γ=180−(α+β)

Mila: z Tw. cosinusów : c²=a²+b²−2ab cosγ⇔2ab*cosγ=a²+b²−c² a²=b²+c²−2bc cosα⇔2bc*cosα=b²+c²−a² dzielę stronami : (Δ jest ostrokątny to prawe strony równości różne od zera⇒lewe też)

2ab*cosγ		a2+b2−c2
	=		⇔
2bc*cosα		b2+c2−a2

a2+b2−c2		a*cosγ		2R sin α*cosγ
	=		=		⇔
b2+c2−a2		c*cosα		2R sinγ*cosα

a2+b2−c2		sinα		cosγ
	=		*		⇔
b2+c2−a2		cosα		sinγ

a2+b2−c2
	=tgα*ctgγ
b2+c2−a2

pigor: Dany jest trójkąt ostrokątny ABC o bokach długości a,b,c i kątach

	a2+b2−c/td>
odpowiednio. Wykaż, że		= tgα ctgγ.
	b2+c2−a2

Mila: Cześć pigor, coś źle napisałam?

pigor: ... , miało być do mojej ... szuflady, ale uciekło mi; przepraszam,