Od Kacpra Benny: Zad 1 Oblicz wartość wyrażenia

	2*cos36o*sin18o*cos18o		2*cos36o*sin36o
cos36o*sin18o=		=		=
	2cos18o		4cos18o

	sin72o		cos18o		1
=		=		=
	4cos18o		4cos18o		4

Zad 2.Oblicz całkowitą wartość parametru p, dla którego równanie 3^2x−4*3^x+p=0 ma dwa rozwiązania. 3^2x−4*3^x+p=0 t=3^x>0 t²−4t+p=0

⎧	Δ≥0
⎨	x1+x2>0
⎩	x1*x2>0

z tego otrzymujemy p∊<0;4> wybieramy całkowite p∊{0;1;2;3;4}

	2x+3
Zad 4. Wyznacz zbiór wartości funkcji f(x)=
	2x+1

2x+3		2
	=1+
2x+1		2x+1

2^x>0, więc najmniejsza wartość mianownika dąży do 1 a największa do nieskończoności

	2
lim→0		=2
	2x+1

	2
lim→∞		=0
	2x+1

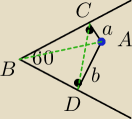
więc nasz zbiór wartości funkcji Zwf=(1;3) Zad 5. Dany jest kąt o mierze 60° oraz punkt A leżący wewnątrz tego kąta. Odległości punktu A od ramion tego kąta są równe a i b. Udowodnij, że odległość punktu A od wierzchołka kąta jest równa

2
	*√(a2+ab+b2)
√3

Suma kątów przeciwległych jest równa 180, więc możemy opisać okrąg, gdzie |AB|=2r z cosinusów |CD|²=a²+b²+ab |CD|=√a²+b²+ab

|CD|
	=|AB|
sin60o

	2
|AB|=		*√a2+b2+ab
	√3

Sprawdź zadanie 3, bo chyba treść jest niepełna Sorry, że dopiero dziś, ale nie miałem wczoraj za bardzo czasu

YushokU: Dlaczego w drugim używasz wzorów Vieta?

Benny: No, a gdybyś miał sytuacje, że x₁= −2, x₂= 3 to ile rozwiązań ma równanie?

Benny: Błąd, t₁ i t₂ tam ma być

YushokU: @Benny No tak.... Nie pomyślałem nawet o tym

Kacper: Tak miało być dwa roziązania całkowite dla p=4 mamy 3^2x−4*3^x+4=0 ⇔ (3^x−2)²=0 ⇔3^x=2 ⇔ x=log₃2 Dla mnie tutaj zbiór rozwiązań jest jednoelementowy To akurat odwieczny problem z liczbą rozwiązań równania kwadratowego....

Kacper: A zadanko 3?

Benny: No, ale gdyby było takie polecenie jak napisałeś wcześniej to jest dobrze? Co do zadanka 3 napisałem wyżej, abyś sprawdził czy wysłałeś mi całe polecenie.

Kacper: Tak zadanie 3 ma dokładnie taką treść: Udowodnij, że jeżeli a>1 i b>1 i log₇a*log₇b=4, to a*b≥2401

Benny: Hmm można tak opuszczać logarytmy? log₇a*log₇b=4 log₇a*log₇b=log₇7⁴ a*b=7⁴ a*b=2401

Kacper: log₂8*log₂4=6 log₂8*log₂4=log₂2⁶ 8*4=2⁶ ?

Saizou : Kacepr warto wykorzystać takie słówko na "ś" tutaj

Benny: łeee, myślałem, że tak szybko pójdzie

Kacper: Saizou dokładnie Kto mnie zna, to wie, że zawsze zaczynamy od tego

Benny: O uwaga coś poszło!

log7a+log7b
	≥√log7a*log7b
2

log27ab
	≥log7a*log7b
4

log27ab
	≥4
4

log²₇ab≥16 / √ log₇ab≥4 log₇ab≥log₇7⁴ ab≥2401

Saizou : tylko niepotrzebnie podnosiłeś do kwadratu Am≥Gm

log7a+log7b
	≥√log7a*log7b=√4=2
2

log₇(ab)≥4=log₇7⁴ ab≥7⁴=2401

Benny: no w sumie

Kacper: Kolejne zadanka?

Benny: Można spróbować.

Kacper: Ok. Zadanie nr 5. Wyznacz zbiór wartości funkcji f(x)=log₂(−x²+x) Zadanie nr 6.

	sinα
Uzasadnij, że jeżeli kąty tójkąta to α,β,γ i		=2cosγ, to trójkąt ten jest
	sinβ

równoramienny. Zadanie nr 7.

	4
Wyznacz zbiór wartości funkcji f(x)=
	sinx+2cosx+3

zadanie nr 8. Wyznacz te argumenty dla których funkcja f(x)=(2−√3)^{(6x−6)/(x+1)} przyjmuje wartości większe niż funkcja g(x)=(2+√3)^−x Zadanie nr 9. Dla jakich wartości parametrów a i b funkcja

	x4−16a
{		dla x≠2
	x−2

f(x)={ {log₂b dla x=2 jest ciągła w R. Zadanie nr 10. Rozwiąż równanie:

	3n2+2n+1
log9x+(log9x)2+(log9x)3+...=limn→∞
	3+6+9+...+3n

Benny: Już myślałem, że nie mam żadnych wolnych kartek do pisania, ale coś się jeszcze znalazło zad 5 już kiedyś ktoś mi dawał f(x)=log₂(−x²+x)

	1		1		1
funkcja wewnętrzna przyjmuje największa wartość dla x=		g(		)=
	2		2		4

	1		1
f(		)=log2		=−2
	4		4

ZWf=(−∞;−2> Zad 6 sinα=sin(180−(β+γ)) sinα=sin(β+γ)

sin(β+γ)
	=2cosγ
sinβ

sinβ*cosγ+sinγ*cosβ=2cosγ*sinβ sin(γ−β)=0 γ=β więc trójkąt równoramienny

Benny: 8. x∊(−∞;−1)∪(2;3) 9. Inaczej niż z de l'Hospitala nie wiem jak ruszyć tej pierwszej granicy. wyszło mi a=1 i b=2³² dziwne wyniki

Kacper: Dotychczas wszystko ok W 9 można myśleć tak: Jeśli g(x)=x⁴−16a ma mieć skończoną granicę w 2, to g(2)=0, czyli a=1

Benny: Zastanawiam się nad tym 4

Kacper: Którym 4?

Eta: 4 maja?

Benny: Oj już mi się nawet numery zadań mylą @Eta 4 maja swoją drogą Chodziło mi o zadanie 7

Mila: Podpowiedź: 9)

	x2−4√a)*(x2+4√a)
limx→2		=
	x−2

	(x−24√a)*(x+24√a)(x2+4√a)
=limx→2		=
	x−2

Benny: Milu rozkładałem tak. W takim przypadku mogę przyjąć, że jeśli granica istnieje to musi dzielić się przez dwumian w tym wypadku (x−2⁴√a)=x−2? Z de l'Hospitala mogę to zrobić tak? H

	x4−16a
limx→2		= limx→24x3=32
	x−2

x⁴−16a=32(x−2) x⁴−16a−32x+64=0 16−16a−64+64=0 16=16a a=1

Mila: Podałam sposób możliwy bez de"H. Oczywiście masz rację, to samo wychodzi. a>0 w moim sposobie. Rozwiązuj teraz bardziej standardowe zadania.

Mila: Dzisiaj idź wcześnie spać.

Mila: Powodzenia.

Benny: Nie dziękuje Najbardziej się tego polskiego obawiam, reszta już pójdzie raczej z górki. Wątpię, że jak pójdę wcześnie spać to zasnę. Już tej nocy słabo spałem. Film jakiś obejrzę przed snem może coś mi to da

Eta: Powodzenia

Benny: Takie ładne jabłuszko, ciekawe czy rano będę w stanie coś zjeść

kix: 5 takich ładnych wróży piękną ocenę

Eta: Matura na 5

kix: czego abiturientowi oczywiście życzę

siema eniu: nic się nie martw majster! relax! idź na piwko albo dwa tylko polski i to ustny budzi lęk w moim sercu,a reszta to bajka! powodzonka dla każdego piszącego!

Marysia: Jak będziecie chcieli, to dzisiaj jeszcze kilka zadań, ale już z poziomu podstawy rozszerzenia

Marysia: Żebyście mi rozwiązali na jutro, bo sama ich nie umiem

Marysia: Też macie taki strach przed polskim jak ja?

Benny: Jakieś zadanka może na podstawę byśmy zrobili?

Benny: Milu masz może jakieś fajne zadanko tak przed maturą?

Mila: 1) rozwiąż układ równań. |x|+|y|=3 2|x|+y=3 2) Trapez o ramionach 6 i 10 jest opisany na okręgu. Odcinek łączący środki ramion dzieli trapez na dwie części , których pola są w stosunku 3:5. Oblicz długosci podstaw tego trapezu.

Mila: 3) f(x)=log_(2cosx)(9−x²) Zapisz dziedzinę f(x) w postaci sumy przedziałów.

Mila: