Wielomiany, równania
Wicio: 1. Ile pierwiastków ma wielomian w(x)=x3−x2−2x+1 w przedziale (−2,2)?
2. Równanie Im−xI + Ix−5I = 9 ma nieskończenie wiele rozwiązań dla?
2 maj 14:54
5-latek: Do zadania nr 1 zastosuj twierdzenie Sturma
2 maj 15:00
Aerodynamiczny: f(x)=x
3−x
2−2x+1
f'(x)=3x
2−2x−2
3x
2−2x−2=0
Δ=4+4*3*2=4+24=28
√Δ=2
√7
| | 2+2√9 | | 1+√7 | | 1−√7 | |
x= |
| = |
| x x= |
| zarówno te 2 x należą do (2;2) czyli ma w nim 2 |
| | 6 | | 3 | | 3 | |
| | 1−√7 | | 1+√7 | |
ekstrema dla x= |
| ekstremum, dla |
| minimum. |
| | 3 | | 3 | |
Sprawdźmy jeszcze jakie wartości są na krańcach przedziałów i w ekstermach,
dla x=−2 wartość jest ujemna,
| | 1−√7 | |
dla x= |
| wartość jest dodatnia |
| | 3 | |
| | 1+√7 | |
dla x= |
| wartość jest ujemna |
| | 3 | |
dla x=2 wartość jest dodatnia
Zatem zaczynamy od ujemnych przechodzi na dodatnie(1rozw), potem przechodzi na ujemne(2rozw) i
na koniec znów na dodatnie(3rozw) zatem w podanym przedziale wielomian ma 3 pierwiastki.
2 maj 15:14
Eta:
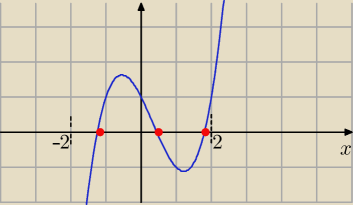
2 maj 15:17
Aerodynamiczny: | | 1−√7 | |
Nie wiem dlaczego napisałem że dla x= |
| jest ekstremum zamiast maksimum. |
| | 3 | |
2 maj 15:17
Aerodynamiczny: W sumie u mnie trzeba by liczyć granice lewo i prawostronne dla 2 i −2, bo są 2 i −2 nie należą
do tego przedziału ale na to samo wyjdzie.
2 maj 15:20
Bogdan:
Proponuję zbadać najpierw liczbę pierwiastków wielomianu Q(x) = W(x) − 1 = x3 − x2 − 2x
i potem podnieść wykres Q(x) o 1 do góry, warto potem sprawdzić niektóre wartości W(x) dla
wybranych wartości x∊(−2, 2)
2 maj 15:27
Aerodynamiczny: W sumie to 2 jakoś dziwnie wyjdzie, wydaje mi się że dobrze robię, ale jak sprawdziłem to nie
do końca. Musze popatrzeć jeszcze. A w tym moim rozwiązaniu powyższym jest trochę błedów
"nieuwagi czasem się zła liczba wkrada, i zamiast v jest x. Trzeba uważać

2 maj 15:34
Aerodynamiczny:
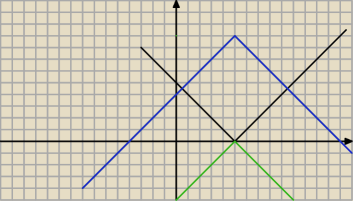
9 − Ix−5I to jest tego wykres(niebieski), moim zdaniem Im−xI nigdy nie pokryje się z tym
wykresem, jedynie w przedziałach to będzie miało nieskończenie wiele rozwiązań dla m=−4(gdy
oba ujemne)i m=14(gdy oba dodatnie)
Mógłby ktoś na to spojrzeć?
2 maj 15:48
Kacper:
Tw Sturma

w liceum?

2 maj 15:50
Bogdan:
y = |x − m|, weź m = −4 oraz m = 14
2 maj 15:51
5-latek: Kacper . W sumie pochodne wrocily , a dzielenie wieolomianow w liceum jest
2 maj 15:57
Aerodynamiczny: Jednak w sumie jak jadłem obiad dotarło do mnie że żeby było nieskończenie wiele rozwiązań nie
muszą się w całości wykresy pokrywać, wystarczy że jakąś cześć w której i tak będzie
nieskończenie wiele rozwiązań.
2 maj 16:09


 9 − Ix−5I to jest tego wykres(niebieski), moim zdaniem Im−xI nigdy nie pokryje się z tym
wykresem, jedynie w przedziałach to będzie miało nieskończenie wiele rozwiązań dla m=−4(gdy
oba ujemne)i m=14(gdy oba dodatnie)
Mógłby ktoś na to spojrzeć?
9 − Ix−5I to jest tego wykres(niebieski), moim zdaniem Im−xI nigdy nie pokryje się z tym
wykresem, jedynie w przedziałach to będzie miało nieskończenie wiele rozwiązań dla m=−4(gdy
oba ujemne)i m=14(gdy oba dodatnie)
Mógłby ktoś na to spojrzeć?
 w liceum?
w liceum? 