Optymalizacja. asdasdqwe: Zadanko na pochodną z Andrzeja Kiełbasy. W stożek, którego przekrojem osiowym jest trójkąt równoboczny wpisano walec o największej objętości. Oblicz stosunek promienia podstawy walca do promienia podstawy stożka. Wychodzi mi zła odpowiedź, proszę jedynie o pomoc w wyznaczeniu funkcji jednej zmiennej, korzystałem tam z podobieństwa ale wynik wyszedł zły, bo ma być 2/3 a mi wyszło 1/2

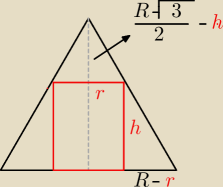
YushokU: Tak zakodujesz r + h, pamiętaj, że to R to jest twoja dana, a nie niewiadoma. Tak liczyłeś?

YushokU: Wychodzi tak:

r√3   −h 2		h
	=
r		R−r

	r√3
(		−h)(R−r)=hr
	2

po wyliczeniu U{r√3{2}+h=U{R√3{2} h=U{√3{2}(R−r) Podstawiasz do wzoru na objętość.

	√3π
V(r)=		(Rr2−r3)
	2

Pochodna i wychodzi. Odpowiedź w zbiorze jest poprawna

YushokU: Zjadłem trochę ułamki, tak to powinno wyglądać w środku.

r√3		R√3
	+h=
2		2

	√3
h=		(R−r)
	2