trapez aha: Punkty B(3;1) i D(−2;2) są przeciwległymi wierzchołkami trapezu równoramiennegoABCD, w którym AB∥CD Prosta o równaniu y=x jest osią symetrii tego trapezu. Oblicz współrzędne wierzchołków A i C oraz pole trapezu. oraz pole tego trapezu. nie mam pojęcia jak to zrobić. czy ta prosta y=x jest prostopadła do podstaw i przechodzi przez środek AB i CD? proszę o pomoc z wierzchołkami, pole już dam radę samodzielnie

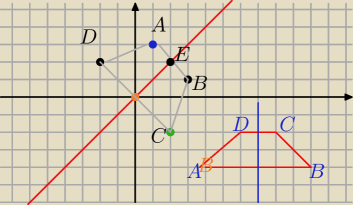
5-latek: Będzie to taka sytuacja Z punktem C nie ma problemu bo znamy wspolrzedne punktu D i wsolrzedne srodka odcinka DC (czyli (0,0) Ze wzoru na srodek odcinka wyliczasz wspolrzedne punktu C Teraz wspolrzedne punktu A Liczymy wspolczynnik prostej prostopadlej do prostej y=x wiec będzie to a=−1 Znamy wspolczynnik kierinkowy i wspolrzedne punktu B wiec piszsemy równanie prostej prostopadlej do y=x i przechodzącej prze punkt B czyli y=(x−x₀)+y₀ gdzie x₀ i y₀ to wspolrzedne punktu B Mamy rownie prostej prostopadlej wiec liczymy ipunkt przciecia tych prostych E Majacwspolrzedne punktu E i B ze wzoru na srodek odcinka policz wspolrzedne punktu punktu A bo jak napisales /as na początku os symetrii jest prostopadla do bokow idzieli je na polowy

5-latek: Nie bokow tylko podstaw.

5-latek: I równanie prostej prostopadlej do y=x i przechodzcej przez B ma postac y=a(x−x₀)+y₀ Zapomnialem tam wcześniej dopisać a Nie było by problemu gdyby a=1 ale tutaj a=−1