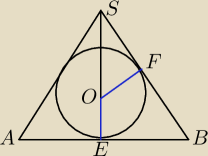
zadanie z kulą wpisaną w ostrosłup - Byłby ktoś tak miły i znalazł błąd :)? początkujący: W czworokatnym ostrosłupie prawidłowym wysokość jest równa 8 cm, krawędź podstawy ma długość 12. Wyznacz promień r kuli wpisanej w ostrosłup i promień R kuli opisanej na ostrosłupie. Narysowałem bardziej "dwuwymiarowe", żeby było bardziej czytelne. póki co zatrzymałem się na r Wiec: AB − przekatna podstawy (kwadratu) ⇒ EB = 6√2 BS² = 8² + (6 √2)² BS = 2p {34} BE = BF ⇒ SF = 2√2 (√17 − 3) Z pitagorasa: r² + SF² = (8−r)² Z tego mi wychodzi r = 3√17 − 9 r powinno się równać 3 byłbym bardzo wdzięczny gdyby ktoś pokazał mi błąd albo inny sposób rozwiązania tego zadania Ps. Przepraszam za brak modułów ale pisze z telefonu

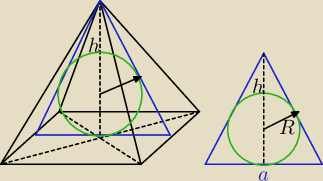dero2005: zrobiłeś zły rysunek, z tego rysunku R = 3

początkujący: Faktycznie; dzięki wielkie