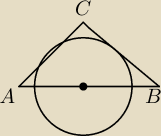
 W półokrąg o środku leżącym na boku AB trójkąta ABC jest styczny do boków AC i BC (zob rys.).
Dla |AC|=13, |BC|=15 i |AB|=14 promień tego półokręgu wynosi
a.3
b. 4
c. 5
d. 6
W półokrąg o środku leżącym na boku AB trójkąta ABC jest styczny do boków AC i BC (zob rys.).
Dla |AC|=13, |BC|=15 i |AB|=14 promień tego półokręgu wynosi
a.3
b. 4
c. 5
d. 6
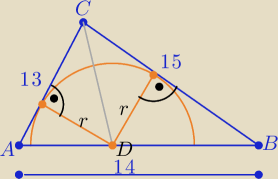
| 1 | 1 | |||
P(ADC)=P1= | 13r i P(ΔDBC=P2= | 15*r | ||
| 2 | 2 |
| 1 | ||
P(ΔABC)= P1+P2= | *28r | |
| 2 |
| a+b+c | ||
P(ΔABC)= √p(p−a)(p−b) (p−c) , p= | ||
| 2 |
| 1 | ||
P(ABC)= | *28r= 14r | |
| 2 |
