Prosta k: 4x+3y-77=0 przecina okrąg tejterin: Prosta k: 4x+3y−77=0 przecina okrąg x² + y² − 20x − 40y +315=0 w punktach A i B oblicz długość ccięciwy AB. Normalnie zadanie zrobiłabym z układem równań i potem długością odcinka AB, ale rachunki są taak koszmarne, że to chyba nierealne, chyba, że coś pokręciłam. Dodam, że to zadanie z kodowaną odpowiedzią, ale i tak cyfry są tragiczne. Jest jakis inny sposób?

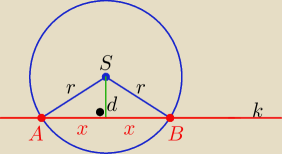
Eta: S(10, 20) , r²= 185 odległość punktu S od prostej k to:

	|10*4+20*3−77|		23
d=		=
	√25		5

z tw. Pitagorasa : x²=√r²−d² =...... ⇒ x=..... 2x=|AB|= ....

tejterin: dziękuje, właśnie o coś takiego mi chodziło

Eta: