dowód geometryczny paulina: Dwusieczna kąta ACB przecina bok AB tego trójkąta w punkcie D. Oznaczmy długości odcinków AC,

	2ab
BC i DC odpowiednio b, a, d. Wykaż, że d<
	a+b

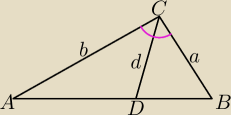
paulina: rysunek:

===: pamiętasz twierdzenie o dwusiecznej? −

paulina:

	b		a
tak,		=		, ale nie wiem jak je wykorzystać
	AD		BD

Marek216: Pewnie chodzi tutaj o nierówność trójkąta ( pewnie − bo nie liczyłem tego), d<b+IADI pozostaje wyznaczyć AD. MOżesz 2 razy zastosować twierdzenie cosinusów i raz twierdzenie o dwusiecznej. Powinno wyjść

Kacper: Marek216 to czekamy na rozwiązanie Zadanie to, jeśli pamiętam jest z OMG

Marek216: Tak jak powiedziałem nie rozwiązywałem tego więc rzuciłem pierwszym lepszym pomysłem, ale skoro dajesz mi wyzwanie to się podejmę Padc+Pbdc=Pabc sry za zapis napisałem tak żeby było wiadomo o co chodzi ( pola trójkątów) Zatem: 1/2 sinx*bd+1/2 sinx*ad=1/2sin2x*ba Z tego mamy: 2sinxcosx=(sinx*BD+sinx*ad)/(b*a) ⇒ cosx=(bd+ad)/(2ba) I teraz trzeba założyć że cosx<1 zatem: (bd+ad)/(2ba)<1 d(a+b)<2ab d<(2ab)/(a+b) I co zadowolony drogi Panie Kacperku?

Kacper: Ujdzie