Sześciokąt równokątny Przemysław: Udowodnij, że suma odległości dowolnego punktu leżącego wewnątrz sześciokąta równokątnego od prostych zawierających jego boki jest stała. Coś czuję, że jest jakieś piękne rozwiązanie. Czy raczej trzeba to rozpisywać dokładnie, te wszystkie równania prostych, odległości i pokazać, że suma nie zależy od współrzędnych punktu, o ile punkt jest w środku? Proszę o pomoc

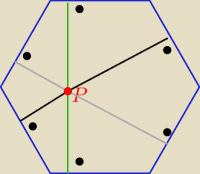
Eta: Odpowiedz na pytanie: Jaka jest odległość między bokami równoległymi w sześciokącie foremnym? i otrzymasz tezę

Przemysław: Racja, ta odległość jest stała. Tylko, że sześciokąt z zadania nie musi być foremny − ma być tylko równokątny.

Eta: A równokątny? to jaki? ............

Przemysław: Każdy kąt 120^o

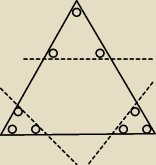
Przemysław: Może powstać przez "ścięcie" z trójkąta równobocznego mniejszych trójkątów, przykład na rysunku. Kółka oznaczają 60^o. Ale wracając do zadania, to chyba nic nie zmieni, bo te boki są dalej równoległe, więc odległość stała?

Przemysław: To nie jest równoważne o ile mi wiadomo

Eta: ok masz rację

Eta:

Eta: Dobrej nocki

Przemysław: Dobranoc! Dziękuję za pomoc

Vax: Podpowiedź: Udowodnij, że suma odległości dowolnego punktu od boków danego trójkąta równobocznego jest stała.

Vax: Oczywiście punktu leżącego wewnątrz trójkąta

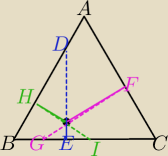
Przemysław: Ta suma odległości x*h₁+y*h₂+z*h₃, gdzie: h₁ − wysokość trójkąta prostokątnego CDE na bok EC h₂ − wysokość trójkąta prostokątnego CGF na bok FC h₃ − wysokość trójkąta prostokątnego BHI na bok BH i te x,y,z są jakoś od siebie zależne. przykładowo: x=1 ⇒ z=0 y=1 ⇒ x=0 z=1 ⇒ y=0 Ale dalej nie mam pomysłu... Na pewno jest lepsza metoda

5-latek: http://www.google.pl/url?sa=t&rct=j&q=&esrc=s&source=web&cd=4&cad=rja&uact=8&ved=0CDYQFjAD&url=http%3A%2F%2Fzadane.pl%2Fzadanie%2F5269019&ei=DdVEVbrCBYO6acPzgegG&usg=AFQjCNHAN63_0FujPaQxnHQWD3qc0cfS5w znalazłem takie cos (bo zainteresowal mnie ten szesciokat rownokatny

Eta:

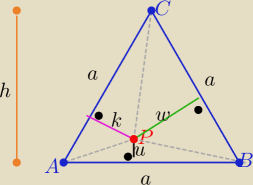
	u*a		k*a		w*a
P1=P(ΔAPB) =		, P2=P(ΔAPC)=		, p3=P(ΔBPC)=
	2		2		2

	a*h
P(ABC)=P1+P2+P3=
	2

...... dokończ

Przemysław:

u*a		k*a		w*a		a*h
	+		+		=
2		2		2		2

ua+wa+ka=ha u+w+k=h=const. Dziękuję Wam za pomoc Tylko jeszcze się zastanawiam: jeżeli mamy, że suma odległości od boków trójkąta równobocznego jest stała, to dlaczego to oznacza, że suma odległości od boków sześciokąta równokątnego jest stała? Rozumiem, że ten 3 z boków sześciokąta leżą na bokach trójkąta, ale nie widzę jak to pomaga

Vax: Zauważ, że masz tam dwa duże trójkąty równoboczne

Przemysław: Prawda! Czyli skoro w dowolnym punkcie każdego z tych trójkątów to również tam gdzie się na siebie nakładają, czyli w tym sześciokącie, tak?

Vax: Trochę niespójnie to napisałeś, no ale mniej więcej tak. Dany sześciokąt należy do obu trójkątów, więc dowolny punkt w nim zawarty leży wewnątrz obu trójkątów, skąd suma jego odległości od boków trójkąta (jednego i drugiego) jest stała, czyli suma tych odległości też jest stała

Przemysław: Dziękuję bardzo