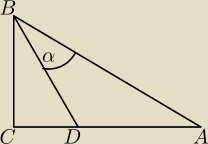
 Dany jest trójkąt prostokątny ABC, w którym kąt ACB jest równy 90 stopni. Punkt D leży na
przyprostokątnej AC.Udowodnij, że jeśli |BC| = 2|CD| oraz |AD| = 5|CD|, to kąt ABD jest równy
45 stopni.
Dany jest trójkąt prostokątny ABC, w którym kąt ACB jest równy 90 stopni. Punkt D leży na
przyprostokątnej AC.Udowodnij, że jeśli |BC| = 2|CD| oraz |AD| = 5|CD|, to kąt ABD jest równy
45 stopni.
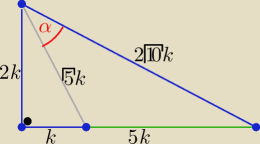 Z tw, kosinusów
Z tw, kosinusów
| 5k2+40k2−25k2 | √2 | |||
cosα= | = | ⇒α=45o | ||
| 2*√5k*2√10k | 2 |