funkcje tarzan:

	1
wykres funkcji f(x)=		został przesunięty tak że jego osiami symetrii są proste o
	x

	1
równaniach y=x−7 i y= −x=3. Po tym przekształceniu wzór funkcji ma postać y=		+q.
	x−p

wyznacz p i q.

5-latek:

	1
jakie proste sa osiami symetrii hiperboli y=		?
	x

narysuj jej wykres i zobacz

tarzan: nie wiem. nie widzę tego. może ktoś pomoże?

Qulka: a jak dokładnie wyglądają te równania?

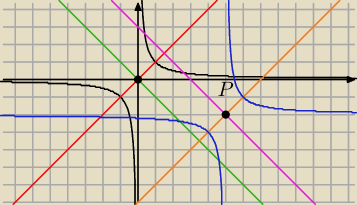5-latek: Teraz widzisz ze sa to proste y=x i y=−x i te proste się przcinaja w punkcie (0,0) Teraz na takim rusunku narysuj sobie te dwie dane twoje proste i wyzna punkt przecięcia się tych prostych P Rozowa y=−x+3 i brazowa y=x−7 (masz punkt przecięcia P=(5,2)

	1
czrny wykres		musisz przesunąć o wektor [5 −2] żeby otrzymać wykres niebieski
	x

Nappisz wzor tej funkcji jeśli go przsuniesz o ten wektor

Lukas: Qulka będziesz dziś po południu, pilne fizyka ! Prosi o pomoc

5-latek: Pewnie chciales to zrobić bez rysunku ? Zapomnij o tym

5-latek: Oczywiście ma być P=(5,−2)

Qulka: 5−latek jakżeś to zrobił przecież to nijak sie ma do treści zadania?

Lukas: Zrobił po swojemu

Qulka: aaa widzę ..niepotrzebnie rysował tę czerwoną i zieloną łatwiej zauważyc by się dało tę symetrię

5-latek: Dzien dobry Aniu Pozdrawiam

Qulka: 5−latku witaj

5-latek:

	1
czyli przepis na nowy wzor funkcji jest taki y=		−2
	x−5

prosta: Witajcie... fajny sposób rozwiązania mi przyszły do głowy " wierzchołki " hiperboli i utonęłabym w rachunkach

5-latek: Dzien dobry prosta