Romb Pati: Miara kąta ostrego rombu jest równa 30^o. Wykaż, że długość boku rombu jest równa średniej geometrycznej długości jego przekątnych. Wyszło mi, że średnia geometryczna przekątnych jest równa a². Niestety nie ma odpowiedzi do tego zadania.

kix: odpowiedź jest OK

Pati: Czyli jak jest polecenie "wykaż, że..." to nie zawsze się da to wykazać? Czyli wykazuje, że ta zależność nie zachodzi?

kix: jak jest polecenie "wykaż, że...." to w/g mnie trzeba wykazać

Pati: No to odpowiedź a² nie jest ok

kix:

	a2
P=a2sinα=
	2

	d1d2
P=
	2

a2		d1d2
	=
2		2

a=√d₁d₂

Alfa: napisz dokładnie co Ci wyszło

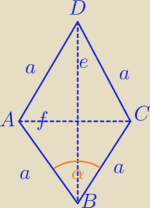
Mila: Masz wykazać, że a=√e*f, gdzie e i f to długości przekątnych.

	a2
P▱=a2*sin(30o)=
	2

	e*f
P▱=
	2

a2		e*f
	=		⇔
2		2

a²=e*f a=√e*f cnw

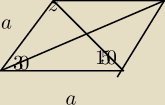
Psycho: źle Ci wyszło niestety. rysuje romb i bok oznaczam jako a, zaznaczam katy kąt ostry mamy podany czyli 30 a kąt rozwarty wyliczamy 180−30=150(bo suma kątów przy ramieniu równa się 180). Teraz korzystamy z Tw.cosinusów: d₁²=a²+a²−2*a*a*cos30⇒d₁=a√(2−√3) d₂²=a²+a²−2*a*a*cos150 →cos150=cos(180−30)=−cos30=−√3/2 czyli d₂=a√(2+√3) Teraz chodzi o ŚREDNIĄ GEOMETRYCZNA (nie arytmetyczną ) a więc korzystamy ze wzory który jest w tablicach maturalnych; √(d₁*d₂)=√(a√(2−√3)*a√(2+√3)=√a²*√(4−3)=√a²=a c.n.u

Psycho: rysunek niestety w pośpiechu jest dość nieudany i uwaga na pierwiastki w ostatnim zapisie bo nie są za bardzo widoczne Mam nadzieję że pomogłam

Pati: Robiłam właśnie z twierdzenia cosinusów tylko zrobiłam, że d₁=a²(2−√3), a nie (d₁)², tak samo z drugą przekątną, stąd wychodziło mi a² zamiast a. Eh, znowu gapiostwo... Dzięki

Mila: Pati przecież masz rozwiązane 21:41.

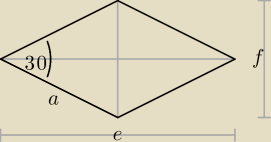
Bogdan: Proponuję w ten sposób rysować romb, zawsze wyjdzie tak jak trzeba. Rozwiązanie Psycho − brrr

Psycho: kix, Mila dobre rozwiązania i łatwiejsze

5-latek: Ale TY tez to zadanie zrobiles i to jest najwazniejszse Tam na końcu powinieneś napisac tak =|a|=a bo a>0 bo masz √a²