udowodnij SiA: Dany jest prostokąt ABCD, w którym IABI > IBCI. Na środku boku AD obrano punkt M,a następnie zbudowano odcinek CM.Punkt P to punkt przecięcia odcinka CM z przekątną prostokąta BD. Wykaż, że IBPI=2IDPI.

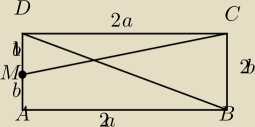
SiA: może teraz z podobieństwa trójkątów ABD i MDC ale nie wiem co to nam da , proszę o jakiekolwiek wskazówki

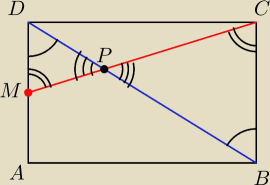
Vuks: Jak zawsze rysunek jest najważniejszy. Na maturze ZAWSZE! rysuj. Nie robiąc tego ryzykujesz błędy. Wracając do zadania. Trójkąty ΔDPM i ΔBPC są podobne na mocy KKK. 2|DM| = |CB| ⇒ |BP|=2|DP|

SiA: Dziękuję ślicznie

Vuks: Co do rysunków − jest opcja cofnij, dzięki której możesz poprawić coś co źle narysowałeś(aś?), chociażby te zachodzące na rysunek oznaczenia wierzchołków. Staraj się również niepotrzebnie nie udziwniać oznaczeń. 2a jest niepotrzebne, wystarczyłoby samo a. Stosowanie różnych kolorów też może czasem pomóc (zwłaszcza w geometrii przestrzennej).

SiA: Następnym razem się postaram

SiA: a mógłbyś mi jeszcze powiedzieć dlaczego w poprzednim zadaniu za X postawiłeś 3 ? mogę podstawić jakąkolwiek liczbę z dziedziny?

Vuks: Dokładnie tak. 3 wybrałem bo wychodziły ładne logarytmy.