ciąg maggiewild: Ciąg (an) jest określony wzorem an = (n + 2)(6− n) dla n ≥ 1 . Liczba dodatnich wyrazów tego ciągu jest równa A) 3 B) 4 C) 6 D) 5 mi wychodzi, że 4, nie wiem czy dobrze? a nawet jak tak, to podzielcie sie waszym sposobem na takie zadania, ach te ciągi

Kacper: Podstawiamy n=1, n=2, n=3, n=4, n=5. Widać, że dla n≥6 drugi czynnik już jest niedodatni, czyli wynik nie będzie dodatni

Kejt: (n+1)(6−n) > 0 n = −1 v n = 6 n ∊ (−1; 6) największa liczba naturalna z tego przedziału to 5.

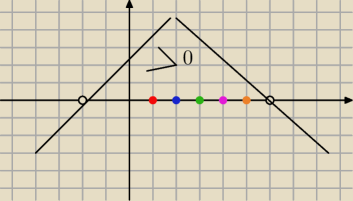
5-latek: widzisz ja mam wlsnie ciag do pan od 40 do 45 lat należy rozwiazac nierownosc (n+2)(6−n)>0 Miejsca zerowe to n+2=0 to n=−2 i 6−n=0 to n= 6 Widzimy z e n*(−n)=−n² wiec ramiona paraboli ida w dol Rysujemy wykres Numery wyrazow naleza do n∊N₊ Wiec jest ich ile ?

5-latek: tak się zastanawiam Kiedy podziekuje za pomoc , bo z ciężkim trudem jej to przychodzi

maggiewild: 5. dzięki wszystkim

maggiewild: nie siedze tu cały czas, więc nie widze kiedy odpowiadacie za każdym razem