Analityczna
Kuba też maturzysta: Udowodnij
a) Udowodnij, że prosta l: 3x + 4y – 19 = 0 jest styczna do okręgów o1 i o2, gdzie
o1: (x – 2)2 + (y – 2)2 = 1 oraz
o2: (x – 6)2 + (y – 4)2 = 9.
b) Obie proste y = 1 i x = 3 są styczne do obu okręgów. Naszkicuj rysunek okręgów o1 i o2,
prostej l, prostej y = 1 i prostej x = 3 w układzie współrzędnych
Znajź równanie 4 stycznej do okręgów o1 i o2. Z tym jest PROBLEM.
1 maj 14:53
+-:
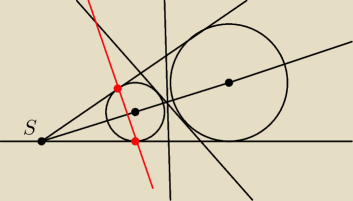
1 maj 17:09
Kuba też maturzysta: a jak z tego równanie wyciągnąć?
1 maj 17:25
+-: Metod jest kilka np.
Prosta przechodząca przez punkty styczności jest prostopadła do prostej przechodzącej przez
środki okręgów i powstają tam przystające trójkąty.
1 maj 17:35
Kuba też maturzysta: skądwiemy, że są prostopadłe?
1 maj 17:48
+-: np Z tego ramiona kąta opisanego są równe do punktów styczności a prosta z wierzchołka przez
środek okręgu jest sieczną, czyli dzieli odcinek między punktami styczności tego kąta na pół.
1 maj 19:08
Vuks:
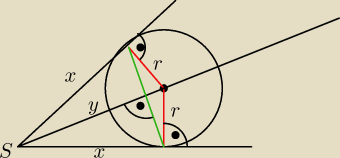
1 maj 19:18

