funkcje toffik: Wykresy funkcji f(x)=ax2+bx+c oraz g(x)=0,5x2+2x+2+m mają wspólną oś symetrii. Funkcja f nie ma miejsc zerowych. Częścią wspólną zbiorów wartości obu funkcji jest przedział <−4,5;−2>. Znajdź współczynniki we wzorze funkcji f i zapisz ten wzór, jeśli wiadomo, że pole trójkąta o wierzchołkach w punktach przecięcia wykresu funkcji g z osią x i wykresu funkcji f z osią y wynosi 18.

===: Fajna "układanka" −

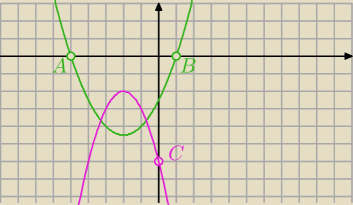
===: ... a zabawię się − wspólna oś symetrii x=−2 − g(x) ma minimum ... ze wspólnej części zbiorów wartości wynika, że ma min=−4,5 −4,5=2−4+2+m ⇒ m=−4,5

	1
ostatecznie g(x)=		x2+2x−2,5
	2

x₁=−5 (a_x) x₂=1 (b_x) − zatem f(x) ma max=−2 − na Oy szukamy punktu C takiego aby trójkąt ABC miał pole równe 18 ⇒ y_c=−6 (to, że znajdujemy go poniżej osi Ox jest oczywiste) − znamy więc już postać kanoniczną f(x) f(x)=a(x+2)²−2 a z niej f(0)=4a−2 −6=4a−2 a=−1 f(x)=−x²−4x−4−2 f(x)=−x²−4x−6 i stąd : a=−1 b=−4 c=−6