2
Ja: zadanie 2
Funkcja kawdratowa f ma dwa miejsca zerowe: −4 oraz 2 i mozna ja opisac wzorem majacym postac
f(x)=ax2+x−4, a≠0 Wykaz, ze najmniejsza wartoscia funkcji f jest −4,5
Czy moze ktos sprawdzic czy merytorycznie dobze rozwiazlem?
f(−4)=16a−4−4=0
a=1/2
f(x)=(1/2)x2+x−4
Jest to funkcja rosnaca wiec najmniejsza wartosc przyjmuje dla wspolrzednej y wierzcholka
paraboli.
delta itd..
q=−4,5
Funkcja jest rosnaca bo wspolczynik przy x2 jest dodatni takie uzasadnienie troche glupio
brzmi, jam myslicie?
30 kwi 21:07
Janek191:
Tak głupio !

a = 0,5 > 0 więc ramiona wykresu są zwrócone ku górze ( f. ma minimum ).
y
min = q = f(p) = f(1) = 0,5*1
2 − 1 − 4 = − 4,5
30 kwi 21:15
5-latek: | | x1+x2 | |
xw=p= |
| x1=−2 i x2= 2 |
| | 2 | |
| | −b | |
p= |
| wyliczysz z tego a |
| | a | |
q= c−ap
2
albo f(p)=q
30 kwi 21:16
Ja: Zamiast ze ramiona sa zwrocone ku gorze to mozna zapisac ze jest rosnaca?
a tutaj z taka funkcja kwadratowa:
f(x)=−x2−2xm−m2−4p
Co powiesz gdy zostaniesz zapytany dlaczego sadzisz ze ramiona paraboli tej funkcji skierowane
sa ku dolowi.
Ramiona wykresu funkcji sa skierowane ku dolowi poniewaz...?
30 kwi 21:24
Ja: 5−latek znam te wzorki. Chodzilo mi o merytoryczne przedstawienie rozumowania tzn. zauwazylem
ze skoro wspolczynnik funkcji jest dodatni to ramiona paraboli funkcji skierowane sa ku dolowi
czyli najwiekszą wartosc funkcja przyjmuje dla wspolrzednej y wierzcholka paraboli.
30 kwi 21:30
Janek191:
a > 0 − ramiona paraboli są skierowane ku górze
a < 0 − ramiona paraboli są skierowane ku dołowi
f(x) = a x2 + b x + c
30 kwi 21:34
prosta:
skierowanie ramion paraboli nie jest określone poprzez monotoniczność funkcji kwadratowej
Funkcja liniowa jest rosnąca lub malejąca w całej swojej dziedzinie,
funkcja kwadratowa jest przedziałami rosnąca lub malejąca
30 kwi 21:35
Ja: Dzieki
30 kwi 21:45
5-latek:
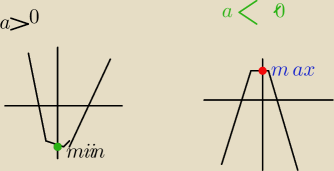
W poleceniu jest napisane ze najmniesza wartość funkcji to (−4,5) a to wskazuje ze
wspolczynnik a >0
30 kwi 22:01
Ja: 5 latek

30 kwi 22:17
 a = 0,5 > 0 więc ramiona wykresu są zwrócone ku górze ( f. ma minimum ).
a = 0,5 > 0 więc ramiona wykresu są zwrócone ku górze ( f. ma minimum ).
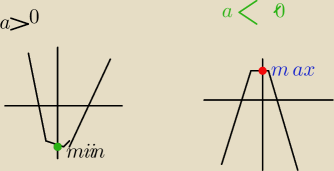 W poleceniu jest napisane ze najmniesza wartość funkcji to (−4,5) a to wskazuje ze
wspolczynnik a >0
W poleceniu jest napisane ze najmniesza wartość funkcji to (−4,5) a to wskazuje ze
wspolczynnik a >0
