2 x pochodne (ciąg, parametr) imprimatur: 1. Ciąg (a, b, c) jest geometryczny i a > 0. Wykaż że funkcja f określona jest wzorem f(x) = x * (ax² + bx + c) jest rosnąca w zbiorze liczb rzeczywistych. 2. Dla jakich wartości parametru m równanie x³ − 3x − m = 0 ma trzy pierwiastki? Rozw: (−2, 2) W pierwszym wiem tyle, że b² = ac, pomnożyłem x przez wyrażenie w nawiasie, wyliczyłem pochodną, wyszło 3ax² + 2bx + c. Dalej nie wiem, liczyłem coś, że f'(x) > 0 i delta = 4b² − 12ac = 4b² − 12b² = −8b²... W drugim wyliczyłem pochodną, wyszły miejsca zerowe −1, 1. Podstawiłem f(−1) = 2 f(1) = −2. Nie wiem jaki warunek musi spełnić, żeby ten przedział wyszedł, proszę o wytłumaczenie. Z góry dziękuje!

Janek191: z.1 f(x) = x*( a x² + b x + c) = a x³ + b x² + c x więc f '(x) = 3a x² + 2 b x + c Δ = 4 b² − 4*3a* c = 4 b² − 12 a*c = 4*( b² − 3a*c) b² > 0 c = a q² > 0 więc Δ < 0 zatem f' (x) > 0 dla x ∊ ℛ i dlatego funkcja f jest rosnąca w ℛ .

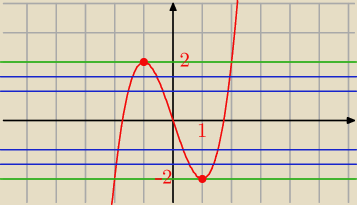
Janek191: z.2 x³ − 3 x − m = 0 f(x) = x³ − 3 x f '(x) = 3 x² − 3 = 3*( x² − 1) = 3*( x − 1)*( x + 1) = 0 ⇔ x = − 1 lub x = 1 f ''(x) = 6 x f ''( − 1) = − 6 < 0 − funkcja f osiąga w punkcie x = − 1 maksimum lokalne y_max = 2 f '' (1) = 6 > 0 − funkcja f osiąga w punkcie x = 1 minimum lokalne y_min = − 2 zatem ZW f = < − 2 , 2 > Prosta y = m przetnie wykres funkcji f 3 razy gdy m ∊ ( − 2 , 2) Patrz też rysunek.

Janek191: Trzeba pominąć : ZWf = < − 2 , 2 >

imprimatur: Kłaniam się nisko! Wielkie dzięki, Janek191! Mam pytanie jeszcze jest równanie trzeciego stopnia z parametrem i pytają się dla jakich wartości m funkcja jest malejąca w R. Sprowadzam to do pochodnej, wychodzi kwadratowa i wiem, że współczynnik a musi być ujemny i pytanie delta mniejsza czy mniejsza lub równa zero?