dowód Rupi: Wykaż, że jeżeli α ,β ,γ są kątami ostrymi i

	1		1		1
sinα=		, sinβ=		, sinγ=		to α + β + γ = 45∘ .
	√5		√26		√65

Rupi: 2.Na bokach AD , AB i BC rombu ABCD wybrano punkty K , L i M w ten sposób, że |AL | : |LB| = k oraz KL ∥ DB , LM ∥ AC . Wyznacz wszystkie wartości k , dla których pole pięciokąta KLMCD

	11
stanowi		pola rombu.
	16

Rupi: Proszę o pomoc

Rupi: ?

Rupi: Wie ktoś

Eta: 1/ trójkąt ostrokątny wyznacz z jedynki trygonometrycznej cosα =.. cosβ=... cosγ=...

	√2
mamy wykazać że α+β+γ= 45o ⇒ sin[(α+β)+γ)=
	2

sin[(α+β)+γ]= sin(α+β)*cosγ+ cos(α+β)*sinγ =........ sin(α+β)= sinα*cosβ+ cosα*sinβ=.... i cos(α+β)= cosα*cosβ−sinα*sinβ=.... i działaj.......... bo mi nie chce się tego pisać

Rupi: Bardzo Ci dziękuję i jestem coraz bardziej zachwycony Twoimi umiejętnościami

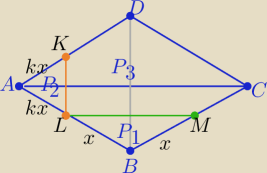
Eta: P−−− pole rombu

	1
P(ΔABC)=P(ΔABD)=		P
	2

	11
P3=		P −− pole pięciokąta
	16

P₁−− pole trójkąta AKL, P₂ −−− pole trójkąta LBM

	5
P1+P2=		P
	16

Z podobieństwa trójkątów: AKL i ABD oraz LBM i ABC

P2		kx		P1		x
	= (		)2 i		=(		)2
P(ABD		kx+x		P(ABC)		kx+x

	1		k2		1		1
P2=		P*		i P1=		P*
	2		(k+1)2		2		(k+1)2

	5
P1+P2=		⇒ ........ 8(k2+1)= 5(k+1)2
	16

rozwiąż teraz to równanie ..............

pigor: ... lub zad.1.np. tak : α,β,γ − miary kątów ostrych , to sin²α= ¹₅ i sin²β=¹₂₆ i sin²γ=¹₆₅, stąd i z 1−ynki tryg. cos²α= ⁴₅ i cos²β=²⁵₂₆ i cos²γ=⁶⁴₆₅, więc tg²α= ¹₅*⁵₄= ¹₄ i tg²β=¹₂₅ i tg²γ=¹₆₄ ⇒

	tgα+tgβ
⇒ tgα=12 i tgβ=15 i tgγ=18 i tg(α+β)=		=
	1−tgαtgβ

	12+15		10		5+2
=		*		=		= 79, zatem
	1−12*15		10		10−1

	tg(α+β)+tgγ
tg(α+β+γ)=tg((α+β)+γ)=		=
	1−tg(α+β)tgγ

	79+18		9*8		7*8+1*9
=		*		=		=
	1−79*18		9*8		9*8−7*1

	56+9		65
=		=		= 1 ⇒ α+β+γ=45o c.n.w.
	72−7		65