rownanie trygonometryczne biednymaturzysta007: rozwiąż równanie {2}{1+4sin²4x)=1−{3}{3+4sin²4x} w przedziale <0,π>

M:

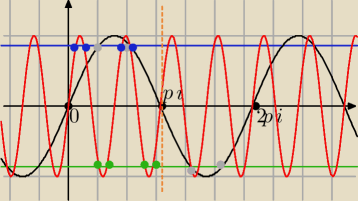
Little Mint: czarny wykres y=sin(x) czerwony wykres y=sin(4x)

2		3
	=1−
1+4sin2(4x)		3+4sin2(4x)

Założenie ;

	1
sin2(4x)≠−		zawsze
	4

	3
sin2(4x)≠−		zawsze
	4

D=ℛ

2		3+4sin2(4x)−3
	=
1+4sin2(4x)		3+4sin2(4x)

2		4sin2(4x)
	=
1+4sin2(4x)		3+4sin2(4x)

6+8sin²(4x)=4sin²(4x)+[4sin²(4x)]² −[4sin²(4x)]²+4sin²(4x)+6=0 [4sin²(4x)]²−4sin²(4x)−6=0 sin²(4x)=t i t∊[0,1] (4t)²−4t−6=0 16t²−4t−6=0 Δ=16+384=400

	4−20		1
t1=		=−		odpada
	32		2

	24		3
t2=		=		dobry jest
	32		4

	3
sin2(4x)=
	4

	√3		√3
1) sin(4x)=		lub 2)sin(4x)=−
	2		2

	π
A) sin(4x)=sin
	3

	π
4x=		+2kπ k∊C
	3

	π		kπ
x=		+
	12		2

	π
Dla k=0 x=		∊[0,π]
	12

	π		π		7π
Dla k=1 x=		+		=		∊[0,π]
	12		2		12

Dla k=2 x∉[0,π] lub

	2π
B)sin(4x)=sin
	3

	2π
4x=		+2kπ k∊C
	3

	π		kπ
x=		+
	6		2

	π
dla k=0 x=		∊[0,π]
	6

	π		π		2π
dla k=1 x=		+		=
	6		2		3

dla k=2 x∉[0,π]

	√3
2) sin(4x)=−
	2

	4π
C) sin(4x)=sin(
	3

	4π
4x=		+2kπ k∊C
	3

	π		kπ
x=		+
	3		2

	π
dla k=0 x=		∊[0,π]
	3

	5π
dla k=1 x=
	6

dla k=2 x∉[0,π] lub

	11π
D) sin(4x)=sin
	6

	11π
4x=		+2kπ i k∊C
	6

	11π		kπ
x=		+
	24		2

	11π
dla k=0 x=		∊[0,π]
	24

	23π
dla k=1 x=		∊[0,π]
	24

k=2 x∉[0,π]

	π		π		π		11π		7π		2π		5π		23π
Odp x∊{		,		,		,		,		,		,		,		}
	12		6		3		24		12		3		6		24

Bardzo bym prosił o sprawdzenie tego rozwiązania . Dziękuje

Little Mint: