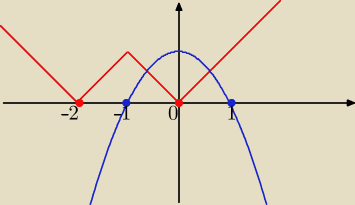
Wyznacz liczbę rozwiązań zadania w zależności od parametru a (a^2+||x+1|-1|=1 Darek: Witajcie, Zmagam się z takim problemem: a² + ||x+1|−1| = 1 Przekształciłem to równanie do ||x+1|−1| = 1 − a² i narysowałem obie strony równania. Niestety, nie mam pojęcia jak wyznaczyć liczbę rozwiązań w zależności od parametru a. Rozwiązanie zadania to: 0 rozwiązań dla a ∊ (−∞; −1) ∪ (1; +∞), 2 rozwiązania dla a ∊ {−1; 1}, 3 rozwiązania dla a ∊ {0}, 4 rozwiązania dla a ∊ (−1,1)\{0} Proszę o wytłumaczenie sposobu wyznaczania ilości rozwiązań. Pierwszy raz przytrafiło mi się zadanie z parametrem wyrażonym w taki sposób. Pozdrawiam

Darek:

Aerodynamiczny: Ja bym to troch inaczej rysował −||x+1|−1| +1 i a² Ale nie traktował "a²" jako parabolę lecz jako prostą.

prosta: nie możemy w jednym układzie rysować wykresu funkcji z wartością bezwzględną ( z argumentem x) i paraboli− funkcji z argumentem a)

Aerodynamiczny: ale a nie jest funkcją , jest parametrem.

prosta: równanie ma 4 rozwiązania, gdy (1−a²)∊(0,1) 3 rozwiązania, gdy 1−a²=1 2 rozwiązania, gdy 1−a²>1 lub 1−a²=0 0 rozwiązanN, gdy 1−a²<0

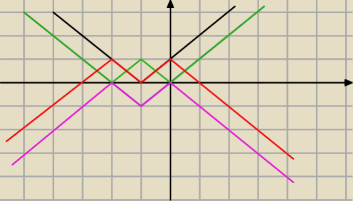
Aerodynamiczny: Czerwony wykres jest wykresem ostatecznym −||x+1|−1| +1 Teraz a² traktujesz jako prostą, 0 rozw. dla a²>1 zatem dla a>1 v a<−1 2 rozw dla a²=1 zatem dla a=−1 v a=1 3 rozw dla a²= 0 zatem dla a=0 4 rozw dla a²<1 zatem dla a<1 i a>1 bez a=0 Wyszło tak jak miało wyjść (wiem że te moje przedziały są niedoskonałe, powinny być takie jak wyżej w odpowiedziach w pierwszym poście ) Mam nadzieję że się rozjaśniło

prosta: ... u mnie po obliczeniach mamy dokładnie to samo

Aerodynamiczny: No tak, moje jest graficzne rozwiązanie Zawsze lepiej mieć kilka sposobów w zanadrzu

Darek: Aerodynamiczny, dziękuję! Nie traktowałem a² jak prostej Wcześniej tak rysowałem, ale nie zgadzało się z odpowiedziami. Dzięki!