rachunek różniczkowy
mamba: ratunku!

Dana jest parabola o równaniu y=x
2 + bx+ c. Prosta o równaniu 5x−y+1=0 jest do niej styczna w
punkcie A, a prosta o równaniu x+y+8=0 jest do niej styczna w punkcie B. Oblicz pole trójkąta
ABC, w którym C jest wierzchołkiem paraboli.
29 kwi 22:36
===:
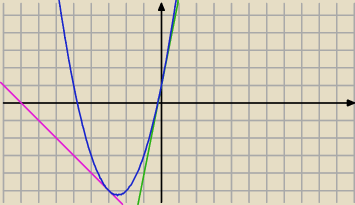
Przyrównując kolejni równanie paraboli i prostej i zakładając Δ=0 (jeden punkt wspólny)
otrzymasz układ dwóch równań i wyliczysz b=5 c=1
Twoja parabola dana jest więc równaniem y=x
2+5x+1
Teraz wyznaczaj wierzchołki trójkąta ABC
29 kwi 22:54
===:
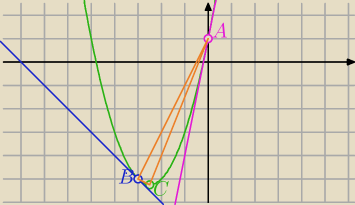
y=x
2+5x+1
y'=2x+5
i teraz przyrównuj to do współczynników danych prostych ... policzysz współrzędne punktów
styczności A i B
2x
A+5=5 ⇒ x
A=0 y
A=1
2x
B+5=−1 ⇒ x
B=−3 y
B=−5
Punkt C to wierzchołek paraboli
x
C=−2,5 y
C=−5,25
Pole to już banał
29 kwi 23:19
 Dana jest parabola o równaniu y=x2 + bx+ c. Prosta o równaniu 5x−y+1=0 jest do niej styczna w
punkcie A, a prosta o równaniu x+y+8=0 jest do niej styczna w punkcie B. Oblicz pole trójkąta
ABC, w którym C jest wierzchołkiem paraboli.
Dana jest parabola o równaniu y=x2 + bx+ c. Prosta o równaniu 5x−y+1=0 jest do niej styczna w
punkcie A, a prosta o równaniu x+y+8=0 jest do niej styczna w punkcie B. Oblicz pole trójkąta
ABC, w którym C jest wierzchołkiem paraboli.
 Przyrównując kolejni równanie paraboli i prostej i zakładając Δ=0 (jeden punkt wspólny)
otrzymasz układ dwóch równań i wyliczysz b=5 c=1
Twoja parabola dana jest więc równaniem y=x2+5x+1
Teraz wyznaczaj wierzchołki trójkąta ABC
Przyrównując kolejni równanie paraboli i prostej i zakładając Δ=0 (jeden punkt wspólny)
otrzymasz układ dwóch równań i wyliczysz b=5 c=1
Twoja parabola dana jest więc równaniem y=x2+5x+1
Teraz wyznaczaj wierzchołki trójkąta ABC
 y=x2+5x+1
y'=2x+5
i teraz przyrównuj to do współczynników danych prostych ... policzysz współrzędne punktów
styczności A i B
2xA+5=5 ⇒ xA=0 yA=1
2xB+5=−1 ⇒ xB=−3 yB=−5
Punkt C to wierzchołek paraboli
xC=−2,5 yC=−5,25
Pole to już banał
y=x2+5x+1
y'=2x+5
i teraz przyrównuj to do współczynników danych prostych ... policzysz współrzędne punktów
styczności A i B
2xA+5=5 ⇒ xA=0 yA=1
2xB+5=−1 ⇒ xB=−3 yB=−5
Punkt C to wierzchołek paraboli
xC=−2,5 yC=−5,25
Pole to już banał