Geometria przestrzenna
Domka: Witam.
Proszę o sprawdzenie zadania.

1) Na powierzchni kuli o promieniu 6cm narysowano okrąg. Ze środka kuli średnicę tego okręgu
widać pod kątem 135
o. Oblicz długość narysowanego okręgu. Wynik przybliż z dokładnością 0,1 i
zakoduj go.
R=6cm
d − średnica okręgu
r − promień okręgu
Liczę z tw. cosinusów; po przekształceniu r=
12R*
√4+√2
L=2πr=3,14*6cm*
√4+√2≈43,8
29 kwi 20:31
Mila:
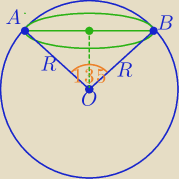
R=6
|AB|
2=6
2+6
2−2*6*6*cos(135
o)
|AB|
2=36+36+72cos(45
o)
|AB|
2=72+36
√2
|AB|
2=36*(2+
√2)
29 kwi 21:37
Domka: Dziękuję

Mam jeszcze problem z zadaniem z geometrii analitycznej i nie wiem co robię źle.
Punkty A=(−1,3), B=(5,1), C=(1,1) są kolejnymi wierzchołkami trapezu prostokątnego. Oblicz
cosα, gdzie α jest miarą kąta rozwartego, zawartego między przekątnymi tego trapezu.
Obliczyłam równanie prostej AB i jest to x+3y−8=0 oraz równanie prostej równoległej do AB,
przechodzącej przez punkt C: x+3y−4=0. Odległość między nimi wynosi 0,4*
√10. Do równania na
odcinek |AD| wstawiam równanie prostej CD (x+3y−4=0) i wychodzi na to, że współrzędna
D=(−1,4;1,8). Liczę długości odcinków AB, CD, AC oraz BD i wstawiam do tw. cosinusów:
(|AB|+|CD|)
2=|AC|
2 + |BD|
2 − 2|AC|*|BD|cosα.
Czy robię gdzieś taki błąd który nie jest błędem obliczeniowym?
29 kwi 22:21
Mila:
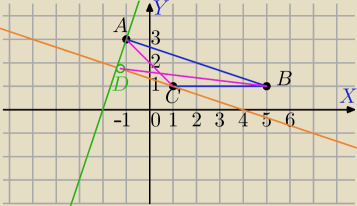
AB: x+3y−8=0
AD:
3(x+1)−1*(y−3)=0
3x+3−y+3=0
3x−y+6=0
CD:
1*(x−1)+3*(y−1)=0
x+3y−4=0
D:
x+3y−4=0
3x−y+6=0
Masz dobrze:
DB
→=[6.4,−0.8]
CA
→=[−2,−2]
Liczysz iloczyn skalarny na dwa sposoby i obliczysz cosα.
30 kwi 16:45
Mila:
30 kwi 20:24
Domka: Dziękuję, chyba znowu błąd jest w książce, bo nie wychodzi mi cosα=−√10/10
30 kwi 20:44
Mila:
Wychodzi dla C=(1,−1) .
Sprawdź, czy dobrze przepisałaś , albo może druk niewyraźny.
30 kwi 21:00
goofie: "Liczę długości odcinków AB, CD, AC oraz BD i wstawiam do tw. cosinusów:
(|AB|+|CD|)2=|AC|2 + |BD|2 − 2|AC|*|BD|cosα."
Mozna w taki sposób zapisać tw. cosinusów? Nie trzeba rozbijać na dwa trojkaty?
30 kwi 21:11
Mila:
A wiesz dlaczego tak zapisałaś?
30 kwi 21:31
Domka: Przesunęłam przekątne i wychodzi trójkąt o kolejnym boku będącym sumą podstaw trapezu (podobny
ze względu na kąty do trójkąta, który składa się z jednej podstawy i części przekątnych). Może
chodziło im o takie współrzędne, jak napisałaś, to zauważyłam, że jest literówka w tekscie.
Mam jeszcze problem z częścią innego zadania; mianowicie pytają mnie, żeby przedstawić pewną
liczbę w postaci potęgi o podstawie 0,2. Co mam zrobić z log50,0016? Wiem, że mogę to
przedstawić jako −log0,20,0016, ale co dalej?
1 maj 14:21
Mila:
1) dobrze.
| | 1 | |
2) log5(0.0016)=c⇔5c=0.0016⇔( |
| )−c=(0.2)4 |
| | 5 | |
c=−4
Może napisz całą treść zadania.
1 maj 16:36
Domka: Ta liczba jest dosyć skomplikowana, więc podam to, co samodzielnie uprosciłam z tym logarytmem.
0,2113*log50,0016
Mam ją przedstawić w postaci potęgi o podstawie 0,2.
1 maj 16:48
Domka: Odpowiedzi mówią, że jest to 0,2117, aczkolwiek nie mam pojęcia jak oni to otrzymali. Pewnie
znowu jakiś błąd w tym zbiorze, nie wiem, jak można takie coś wydać...
1 maj 16:50
Kacper:
Tw. o zamianie podstaw logarytmu

1 maj 16:51
Domka: Nie widzę tego.
1 maj 16:54
Kacper:
0,2113*log50,0016 ta liczba tak?
1 maj 17:06
Domka: Tak, po częściowym przekształceniu. Nie wiem co zrobić z tym logarytmem, bo to jest −4. Jak
przedstawić −4 za pomocą 0,2?
1 maj 17:25
Kacper:
No to będzie ciężko.
Podaj całą treść zadania, to sprawdzę czy odpowiedź w książce jest ok.
1 maj 17:28
Domka: Rozłożę liczbę na 3 części:
a=9√(0,008)169
b=log50,0016
c=(125)−853
Dana liczba to abc. Przedstaw ją w postaci potęgi o podstawie 0,2.
1 maj 17:40
Mila:
Wartość logarytmu jest ujemna, a wartość wyrażenia dodatnia, szukaj błędu w druku, skonsultuj
się z kimmś, kto ma tę samą książkę z innego wydania.
1 maj 21:06
 1) Na powierzchni kuli o promieniu 6cm narysowano okrąg. Ze środka kuli średnicę tego okręgu
widać pod kątem 135o. Oblicz długość narysowanego okręgu. Wynik przybliż z dokładnością 0,1 i
zakoduj go.
R=6cm
d − średnica okręgu
r − promień okręgu
Liczę z tw. cosinusów; po przekształceniu r=12R*√4+√2
L=2πr=3,14*6cm*√4+√2≈43,8
1) Na powierzchni kuli o promieniu 6cm narysowano okrąg. Ze środka kuli średnicę tego okręgu
widać pod kątem 135o. Oblicz długość narysowanego okręgu. Wynik przybliż z dokładnością 0,1 i
zakoduj go.
R=6cm
d − średnica okręgu
r − promień okręgu
Liczę z tw. cosinusów; po przekształceniu r=12R*√4+√2
L=2πr=3,14*6cm*√4+√2≈43,8
 R=6
|AB|2=62+62−2*6*6*cos(135o)
|AB|2=36+36+72cos(45o)
R=6
|AB|2=62+62−2*6*6*cos(135o)
|AB|2=36+36+72cos(45o)
 Mam jeszcze problem z zadaniem z geometrii analitycznej i nie wiem co robię źle.
Punkty A=(−1,3), B=(5,1), C=(1,1) są kolejnymi wierzchołkami trapezu prostokątnego. Oblicz
cosα, gdzie α jest miarą kąta rozwartego, zawartego między przekątnymi tego trapezu.
Obliczyłam równanie prostej AB i jest to x+3y−8=0 oraz równanie prostej równoległej do AB,
przechodzącej przez punkt C: x+3y−4=0. Odległość między nimi wynosi 0,4*√10. Do równania na
odcinek |AD| wstawiam równanie prostej CD (x+3y−4=0) i wychodzi na to, że współrzędna
D=(−1,4;1,8). Liczę długości odcinków AB, CD, AC oraz BD i wstawiam do tw. cosinusów:
(|AB|+|CD|)2=|AC|2 + |BD|2 − 2|AC|*|BD|cosα.
Czy robię gdzieś taki błąd który nie jest błędem obliczeniowym?
Mam jeszcze problem z zadaniem z geometrii analitycznej i nie wiem co robię źle.
Punkty A=(−1,3), B=(5,1), C=(1,1) są kolejnymi wierzchołkami trapezu prostokątnego. Oblicz
cosα, gdzie α jest miarą kąta rozwartego, zawartego między przekątnymi tego trapezu.
Obliczyłam równanie prostej AB i jest to x+3y−8=0 oraz równanie prostej równoległej do AB,
przechodzącej przez punkt C: x+3y−4=0. Odległość między nimi wynosi 0,4*√10. Do równania na
odcinek |AD| wstawiam równanie prostej CD (x+3y−4=0) i wychodzi na to, że współrzędna
D=(−1,4;1,8). Liczę długości odcinków AB, CD, AC oraz BD i wstawiam do tw. cosinusów:
(|AB|+|CD|)2=|AC|2 + |BD|2 − 2|AC|*|BD|cosα.
Czy robię gdzieś taki błąd który nie jest błędem obliczeniowym?
 AB: x+3y−8=0
AD:
3(x+1)−1*(y−3)=0
3x+3−y+3=0
3x−y+6=0
CD:
1*(x−1)+3*(y−1)=0
x+3y−4=0
D:
x+3y−4=0
3x−y+6=0
AB: x+3y−8=0
AD:
3(x+1)−1*(y−3)=0
3x+3−y+3=0
3x−y+6=0
CD:
1*(x−1)+3*(y−1)=0
x+3y−4=0
D:
x+3y−4=0
3x−y+6=0
