Parametry równania + pochodna Bronka: Dla jakich wartości parametru p równanie x³ +3px − p² = 0 ma trzy różne rozwiązania?

M:

Little Mint: Równanie sześcienne jest w postaci x³+px+q=0 Wyróżnik (Δ) tego równania na postac

	4p3
Δ=q2+
	27

Równanie to ma : 1) trzy rózne rozwiązania rzeczywiste gdy jego wyróżnik(Δ) jest mniejszy od zera x³+3px−p²=0 Nasz wyróznik ma postac

	4(3p)3
Δ=p4+
	27

	4*27p3
Δ=p4+		=p4+4p3
	27

p³(p+4)=0 p=0 potrójny p=−4 pojedynczy p⁴+4p³<0 dla p∊(−4,0) Dla p∊(−4,0) równanie x³+3px−p²=0 ma trzy rózne rozwiązania rzeczywiste

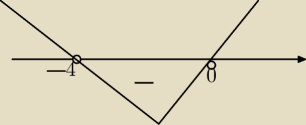
wredulus_pospolitus: alternatywne podejście: f(x) = x³ + 3px − p² 1. f'(x) = 3x² + 3p −−−> f'(x) = 0 ⇔ x² = −p −−−> p < 0 (wtedy mamy jedno maksimum i jedno minimum lokalne −> co jest pierwszym warunkiem do tego abyśmy mogli mieć 3 miejsca zerowe dla funkcji f(x) ) 2. jako, że współczynnik przy najwyższej potędze > 0 to: f(max lokalne) = f(p) = p³ + 3p² − p² = p³ − 3p² = p²(p−3) musi być > 0 −−−−> p < 3 ∧ p ≠ 0 f(min lokalne) = f(−p) = −p³ − 3p² − p² = −p²(p+4) musi być < 0 −−−> p > 4 3. co daje nam ostatecznie przedział p ∊ (−4 ; 0)