Pole trapezu
Dawid: Witam, mam problem z zadaniem:
Punkty A(−1,−2), B(5,2), C(0,4) i D(−3,2) są wierzchołkami trapezu ABCD. Oblicz pole tego
trapezu.
Tak wiec, wykonuję obliczenia:
Długość podstawy AB:
|AB| = √(5+1)2 + (2+2)2 = √62 + 42 = √52 = 2 √13
Długość podstawy DC:
|DC} = √(−3−0)2 + (2−4)2 = √(−3)2 + (−2)2 = √13
Potrzebuje wysokość więc licze równanie prostej zawierające punkty A i B:
y = ax + b
−a + b = −2 /*(−1)
5a + b = 2
a − b = 2
Zatem 6a = 4
a = 2/3
2/3 − b = 2
b = −1/3
y = 2/3x − 1/3
Sprowadzam do ogólnej:
−2/3x + y + 1/3 = 0 /*(3)
−2x + 3y + 1 = 0
licze odległość punktu D od prostej
d = |(Ax + By + C)|/√A2 + B2
d = |(−2*(−3) + 3*2 + 1)|/√(−2)2 + 32
d= 13/√13
po usunięciu niewymierności mam √13
Skoro mam wszystko co potrzeba licze pole:
P=[(a+b)*H]/2
P=(2√13 + √13)* √13/2
P=3√13 * √13 / 2
P= 39/2
P=19,5
Problem w tym, że w odpowiedziach mam wynik 24, kombinowałem na przeróżne sposoby ale zawsze
kończę na swoim. Gdzie mam błąd? Prosze o pomoc. Pozdrawiam!
29 kwi 15:01
===:
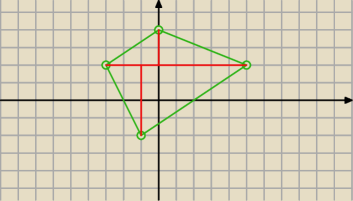
29 kwi 15:09
===:
tak to jest jak nie chce się zrobić rysunku −

29 kwi 15:10
Dawid: Hmmm, jak się podzieli na trójkąty to faktycznie wychodzi, ale skoro to zadanie jest za 5
punktów to nie jestem pewien czy takie rozwiązanie by zaliczyli

Dziękuję

29 kwi 15:32
===:
Przecież nie podaję Ci tego jako rozwiązanie ... prosiłeś o sprawdzenie.
Gdybyś zrobił rysunek lepiej dobierałbyś ścieżkę rozwiązania.
Na maturze czas to pieniądz −

29 kwi 15:34
===:
zauważ na rysunku, że równanie prostej przez A i B policzyłeś z błędem
29 kwi 15:39
Dawid: Rysunek mam w zeszycie, w każdym razie moim sposobem powinien wyjść taki sam wynik, a nie
wychodzi

Dowiedzialbym się, gdzie jest w nim błąd i zamykam temat

29 kwi 15:47


 Dziękuję
Dziękuję 

 Dowiedzialbym się, gdzie jest w nim błąd i zamykam temat
Dowiedzialbym się, gdzie jest w nim błąd i zamykam temat 