Proszę o pomoc.
Somerset: Jedna z podstaw trapezu wpisanego w okrąg o promieniu 3 jest średnicą tego okręgu. Oblicz pole
| | 2 | |
trapezu, jeśli cosinus jego kąta ostrego jest równy |
| |
| | 3 | |
29 kwi 14:46
Somerset:
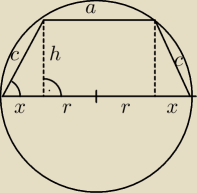
r = 3
2r = 6
Na razie tyle udało mi się zrobić i mi przystawiło. Nie jestem przekonanny czy dobrze
narysowałem i czy dobrze robię obliczenia.
29 kwi 14:51
===:
i z czym masz problem?
29 kwi 14:52
J:
| | 2 | |
z tw cosinusów: r2 = r2 + c2 − 2rc* |
| |
| | 3 | |
29 kwi 14:55
Somerset: Nie wiem co mogę teraz liczyć.
Powinienem wyliczyć c? Czy a?
29 kwi 14:56
J:
wylicz : c , potem a
29 kwi 14:56
Somerset: a = 6
Tak mi wyszło.
Ale czy to możliwe, żeby górna podstawa miała tyle co dolna? Musiałem chyba gdzieś się pomylić.
29 kwi 15:02
Somerset: A mój błąd. Znalazłem. Spróbuję teraz jeszcze raz.
29 kwi 15:04
J:
niemożliwe ... licz dalej , jeśli sie nie pomyliłem, to: a = 2
29 kwi 15:06
Somerset: Korzystasz z tego?
4c = 18 − 3a
?
29 kwi 15:12
J:
z twierdzenia cosinusów (14:55) wylicz c ... dopiero potem a
29 kwi 15:16
Somerset: Nie mogę jakoś pojąć do jakiego trójkąta używasz to tw cosinusów.
r2 to jest promień okręgu, c to jest ramię.
No i nie mogę pojąć jak to wszystko połączyłeś.
Pomyślę jeszcze jak wrócę wieczorem. Ale geometria nigdy nie szła ze mną w parze, nie widzę
tego wszystkiego.
Dziękuję za pomoc!
29 kwi 15:20
 r = 3
2r = 6
r = 3
2r = 6