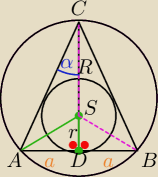
www huhuhu: Wykaż,że jeżeli promień okręgu opisanego na trójkącie równoramiennym jest dwa razy dłuższy od promienia okręgu wpisanego w ten trójkąt, to trójkąt ten jest równoboczny.

	α
∡DAS = 1/2∡DAC = 1/2(90−α) = 45 −
	2

SD
	= tg∡DAS
AD

SD		α
	= tg(45 −		)
a		2

	α
SD = r = a*tg(45 −		)
	2

r =

	α   α   sin45cos − cos45sin   2   2
a*		=
	α   α   cos45cos + sin45sin   2   2

	α   α   cos − sin   2   2
a*		=
	α   α   cos + sin   2   2

	α   α   (cos − sin )2   2   2
a*		=
	α   α   cos2 − sin2   2   2

	α   α   1 −2cos sin   2   2
a*		=
	α   α   cos2 − sin2   2   2

	1 −sinα
a*
	α   α   cos2 − sin2   2   2

jak się pozbyć mianownika?

J: M = cosα

huhuhu: dzięks