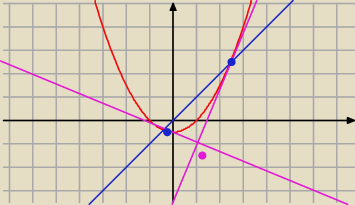
Ktoś coś pomoze ? edna: Prosta o równaniu y=kx przecina parabolę o równaniu y=1/2x²−1/2 w punktach A i B.Udowodnij,ze styczne do tej paraboli w punktach A i B są prostopadłe.

J: wykaż,że f'(x₁)*f'(x₂) = − 1 , gdzie x₁,x₂ to odcięte punktów przecięcia prostej i paraboli

Janek191: y = 0,5 x² − 0,5 y = k x więc k x = 0,5 x² − 0,5 0,5 x² − k x − 0,5 = 0 / *2 x² −2k x − 1 = 0 Δ = 4 k² + 4 = 4*(k² + 1) √Δ = 2√k² + 1

	2k − 2√k2 + 1
x =		= k − √k2m + 1
	2

	2k + 2√k2 + 1
lub x =		= k + √k2 + 1
	2

Styczne y ' = x a₁= k − √k² + 1 oraz a₂ = k + √k² + 1}{2} zatem a₁*a₂ = ( k − √k² + 1)*( k + √k² + 1) = − 1 więc proste styczne są prostopadłe.

Janek191: Ta literka m pod znakiem pierwiastka jest zbędna