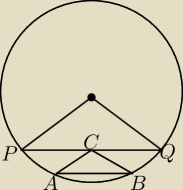
Cięciwa PQ długości 8√2 podzieliła koło o promieniu 4√3 na dwa odcinki kołowe. JA :D: Cięciwa PQ długości 8√2 podzieliła koło o promieniu 4√3 na dwa odcinki kołowe. W odcinek kołowy, który nie zawiera środka koła, wpisujemy trójkąty równoramienne ABC tak, że podstawa AB jest równoległa do cięciwy PQ, a wierzchołek C jest środkiem tej cięciwy. Wyznacz długości boków tego z trójkątów, który ma największe pole.

JA :D: Pomoże mi ktoś ?

JA :D: zrobilem cos takiego. CB=w 1/2AB=x wysokosc z punktu C na AB to y dlugosc odcina srodek kola i punkt C = 4 r²=(4+y)²+x² x²=−y²−8y+32 y²+x²=w² y²+(−y²−8y+32)=w² w²=−8y+32 x²+y²=(−8y+32)² z tego wyznaczam x i podstawiam do wzoru na pole P=1/2*2xy ale nic mi z tego nie wychodzi pomoze ktos?

===: ... pogadaj z tartacznikami ... on tak liczą sprzęgi i "odkrycia" desek −

noixdecoco: A dlaczego w ten sposób wyznaczyłeś x?