objętość
ala: Przekoątna graniastosłupa prawidłowego czworokątnego ma długość 25cm i tworzy z krawędzią
podstawy kąt α taki ze sinα=0,96. Oblicz objętość tego graniastosłupa.
3 gru 17:40
Basia: Pomagam
3 gru 18:07
Basia:
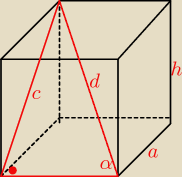
d=25
sinα=0,96=
96100 =
4850 =
2425
sinα=
cd
0,96 =
c25
c = 25*0,96=25*
2425=24
sin
2α+cos
2α=1
| | 242 | | 252−242 | | (25−24)(25+24) | | 49 | |
cos2α=1− |
| = |
| = |
| = |
| = |
| | 252 | | 252 | | 252 | | 252 | |
cosα=
725
cosα=
ad
725=
a25
a =
725*25 = 7
a
2+h
2=c
2
7
2+h
2=24
2
h
2 = 24
2−7
2 = 576−49=527
h =
√527
V = a
2*h = 7
2*
√527 = 49
√527
3 gru 18:18