 1.Funkcja f opisana jest za pomocą zbioru par uporządkowanych
{(−10,6),(−7,4),(−1,0),(0,−5),(1,−8),(3,−8),(5,−9)}. Wobec tego: (ODP C)
A miejscem zerowym funkcji f jest punkt (−1,0)
B funkcja f jest stała
C funkcja f jest monotoniczna
D funkcja f jest różnowartościowa
~moje pytanie~ wiem, że funkcja jest monotoniczna, dlaczego jednak odp A jest nieprawidłowa?
2. Dziedziną funkcji f(x)=|x|−4 jest zbiór liczb całkowitych. Wobec tego: (ODP D)
A wartości funkcji są liczbami naturalnymi
B wykres funkcji nie ma z osią OY punktów wspólnych
C miejscem zerowym funkcji jest punkt (4,0)
D dla pewnego argumentu funkcja przyjmuje wartość równą −1
~moje pytanie~ wiem dlaczego odp D jest prawidłowa... ale dlaczego C jest źle ?
3. Funkcja f opisana jest wzorem f(x)= √x .Zatem: (ODP C)
A dziedziną funkcji f jest zbiór liczb całkowitych
B funkcja f nie ma miejsc zerowych
C dla argumentu 3 funkcja f przyjmuje wartości √3
D funkcja f przyjmuje tylko wartości dodatnie
~moje pytanie~ dlaczego również nie odp B?
1.Funkcja f opisana jest za pomocą zbioru par uporządkowanych
{(−10,6),(−7,4),(−1,0),(0,−5),(1,−8),(3,−8),(5,−9)}. Wobec tego: (ODP C)
A miejscem zerowym funkcji f jest punkt (−1,0)
B funkcja f jest stała
C funkcja f jest monotoniczna
D funkcja f jest różnowartościowa
~moje pytanie~ wiem, że funkcja jest monotoniczna, dlaczego jednak odp A jest nieprawidłowa?
2. Dziedziną funkcji f(x)=|x|−4 jest zbiór liczb całkowitych. Wobec tego: (ODP D)
A wartości funkcji są liczbami naturalnymi
B wykres funkcji nie ma z osią OY punktów wspólnych
C miejscem zerowym funkcji jest punkt (4,0)
D dla pewnego argumentu funkcja przyjmuje wartość równą −1
~moje pytanie~ wiem dlaczego odp D jest prawidłowa... ale dlaczego C jest źle ?
3. Funkcja f opisana jest wzorem f(x)= √x .Zatem: (ODP C)
A dziedziną funkcji f jest zbiór liczb całkowitych
B funkcja f nie ma miejsc zerowych
C dla argumentu 3 funkcja f przyjmuje wartości √3
D funkcja f przyjmuje tylko wartości dodatnie
~moje pytanie~ dlaczego również nie odp B?
| 3x−6 | ||
4. Dziedziną funkcji f określanej f(x) = | jest zbiór (2,+∞) Wobec tego zbiorem | |
| |2−x| |

| 3(x−2) | ||
f(x) = | ||
| x−2 |
 , żartuje.
Pobawmy sie w wykluczanie.
1D−interpretacja graficzna funkcji różnowartościowej: funkcja jest różnowartościowa gdy
dowolnie narysowana prosta pozioma przecina tylko jeden punkt wykresu a tu masz −8 dla dwóch
argumentów, czyli prosta pozioma przetnie 2 punkty
, żartuje.
Pobawmy sie w wykluczanie.
1D−interpretacja graficzna funkcji różnowartościowej: funkcja jest różnowartościowa gdy
dowolnie narysowana prosta pozioma przecina tylko jeden punkt wykresu a tu masz −8 dla dwóch
argumentów, czyli prosta pozioma przetnie 2 punkty  , albo możesz nawet to osbie wziąć na
logikę skoro różnowartościowa to wartości sie nie powtarzają
B−stała byłaby gdyby miała dla każdego argumentu te same wartości
A−miejsce zerowe to nie punkt a argument czyli miejsce zerowe to x=−1
, albo możesz nawet to osbie wziąć na
logikę skoro różnowartościowa to wartości sie nie powtarzają
B−stała byłaby gdyby miała dla każdego argumentu te same wartości
A−miejsce zerowe to nie punkt a argument czyli miejsce zerowe to x=−1
 Dzięki
Dzięki
| x+k | ||
Wykres funkcji f(x)=3x−2 oraz g(x)= | przecinają oś OY w tym samym punkcie. Zatem | |
| x2+1 |
| 0+k | ||
−2= | ||
| 02+1 |
 Do zapamiętania
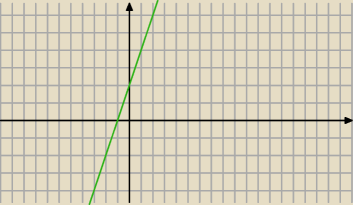
wzor funkcji liniowej jest taki y=ax+b i wlasnie ten wspolczynnik b informuje nas w jakim
punkcie wykres funkcji przecina os OY
np. y=2x+2 (widzisz ze przecial wykres tej funkcji os oY w 2
Do zapamiętania
wzor funkcji liniowej jest taki y=ax+b i wlasnie ten wspolczynnik b informuje nas w jakim
punkcie wykres funkcji przecina os OY
np. y=2x+2 (widzisz ze przecial wykres tej funkcji os oY w 2
