planimetria
maturzysta: | | π | |
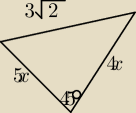
W trójkącie jeden z boków ma długość 3√2, a kąt naprzeciw tego boku ma miarę |
| . Miary |
| | 4 | |
pozostałych dwóch kątów pozostają w stosunku 4:5. Wówczas:
A.kąty trójkąta mają 45,50,85st
B.pole tego trójkąta wynosi 9/2
√6sin75
o
C.jeden z boków trójkąta ma długość 8
√3
D.obwód tego trójkąta jest równy 9 + 3
√2
z twierdzenia sinusow wychodzi ze
tylko jak wtedy reszte tego policzyć?
4x/ siny = 6
5x/ sinz = 6
tak jakos srednio mi to pasuje : /
Eta:
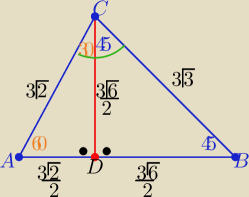
4α+5α= 180
o−45 ⇒ α= 15
o
to: |∡A|=60
o |∡C|=75
o
korzystając ze związków miarowych w trójkątach
ACD o kątach 30
o,60
o, 90
o i w ΔDBC o kątach 45
o, 45
o, 90
o
wyznaczamy długości boków trójkąta ABC
to
| | 1 | | 9 | |
P= |
| *3√2*3√3*sin75o= |
| √6*sin75o |
| | 2 | | 2 | |
odp: B)
