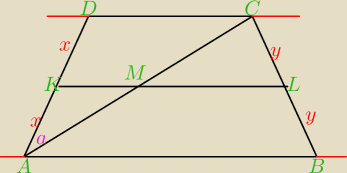
dowod msp: Dany jest trapez ABCD, w którym poprowadzono przez środki ramion prostą równoległą do podstaw AB i CD. Prosta ta przecięła ramię AD, ramię BC i przekątną AC odpowiednio w punktach K,L,M.

	|KM|		|CD|
Wykaż, że		=		.
	|ML|		|AB|

Czy mój dowód jest dobry

|AK|		|KM|		|KA|		|AM|
	=		z podobieństwa trójkątów ΔAKM~ΔADC		=		i
|AD|		|DC|		|KD|		|MC|

kąt a jest taki sam dla obu trójkątów

|CL|		|ML|
	=
|CB|		|AB|

|AK|		|CL|		1
	=		=		więc
|AD|		|CB|		2

|ML|		|KM|
	=
|AB		|DC|

|ML|*|DC|=|AB|*|KM|

|CD|		|KM|
	=
|AB|		|ML

msp: czy mógłby ktoś rzucić okiem będę bardzo wdzięczny

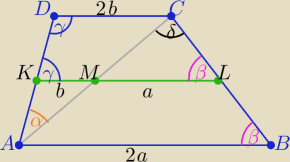Eta: Może być Można było wykazać prościej tak: |AB|=2a i |DC|=2b Z podobieństwa trójkątów ADC i AKM oraz ABC i MLC z cechy (kkk) w skali k=2 mamy: |KM|=b i |ML|=a

|KM|		b		|DC|		2b		b
	=		i		=		=
|ML|		a		|AB|		2a		a

	|KM|		|DC|
to :		=
	|ML|		|AB|

c.n.w

msp: dziekuje