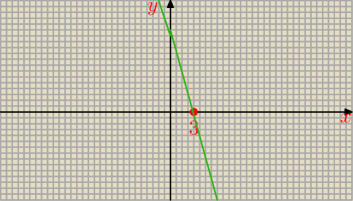
Wykres pochodnej problem Stupid: Na poniższym wykresie przedstawiono wykres pochodnej ′ f (x) funkcji kwadratowej f(x ) . Wykaż, że f (5) < f(2) . Nie mam pomysłu jak się do tego zabrać.

J: w jakim punkcie przecina oś OY ?

Stupid: http://img.zadania.info/zes/1/0097891/HzesT29x.gif

===: ... punkt przecięcia z Oy nie jest tu do niczego potrzebny −

Stupid: Jakieś wskazówki?

Aerodynamiczny: W 3 będziesz miał ekstremum, zastanów się jaki kształt miała parabola, której pochodna wygląda tak jak na rysunku

===: 1) Prosta przedstawiająca pochodną "mówi", że: − Parabola "obrazująca" funkcję jest "smutna" ...ramiona w dół − wierzchołek ma dla x_w=3 zatem x=3 jest jej osią symetrii i wszystko jasne −

Saizou : Niech f(x)=ax²+bx+c, wówczas f'(x)=2ax+b , gdzie a<0, bo wykres pochodnej jest malejący wiemy też że f'(3)=0 zatem 0=6a+b⇒−6a=b stąd f(x)=ax²−6ax+c licząc f(5)=25a−30a+c=c−5a oraz f(2)=4a−12a+c=c−8a , skoro a<0 to f(5) < f(2)

Stupid: Dzięki już ogarnięte