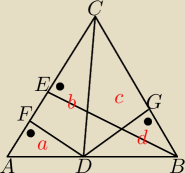
dowod msp: Wykaż, że w trójkącie równoramiennym suma odległości dowolnego punktu podstawy od ramion trójkąta jest równa jednej z wysokości tego trójkąta. Czy mogę wykazać to w następujący sposób |AF|+|FC|=|BG|+|GC| Pole trójkąta ADF=a , PΔFDC=b, PΔDBG=d, PΔDGC=c. a+b+c+d=PΔABC ΔADF ma tę samą wysokość h₁ co ΔFDC, a ΔDBG ma tę samą wysokość h₂ co ΔDGC

|AF|*h1		|FC|*h1		|BG|*h2		|GC|*h2
	+		+		+		=PΔABC
2		2		2		2

h1(|AF|+|FC|)		h2(|BG|+|GC|)
	+		=PΔABC
2		2

|AF|+|FC|=|BG|+|GC|

h1(|AF|+|FC|)		h2(|AF|+|FC|)
	+		=PΔABC
2		2

(|AF|+|FC|)(h1+h2)
	=PΔABC
2

(|AF|+|FC|)(h1+h2)		|EB|*(|AF|+|FC|)
	=
2		2

skracamy i otrzymujemy (h₁+h₂)=|EB|

Eta:

	1		1
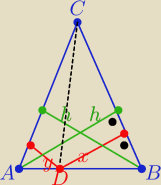
P(ABC)=		|BC|*h i P=		|AC|*h
	2		2

	1		1
P(ABC)=		*x*|BC|+		*y*|AC| i |AC|=|BC|
	2		2

	1		1
to P(ABC)=		*|BC|(x+y) i P(ABC)=		|BC|*h ⇒ x+y=h
	2		2

c.n.u

Braun: Eta robisz postępy

msp: czy mój sposób jest zły

Eta: Też dobry ........... ( ujdzie w tłumie

Eta: @Braun .... co się tak na mnie uwziąłeś?

Braun: Ja ? Ja tylko podziwiam kunszt