Rownanie stycznej do paraboli nick: Dwa boki trojkata rownoramiennego sa zawarte w osiach ukladu wspolrzednych, a prosta zawierajaca trzeci bok tego trojkata jest styczna do paraboli o rownaniu y=¹₂x²+3x+¹¹₂. Oblicz pole tego trojkata. Rozwaz wszystkie przypadki.

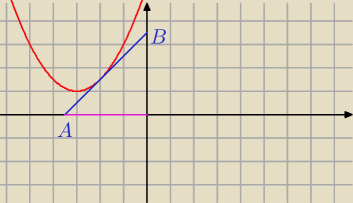
Janek191: 1) y = x + b więc x + b = 0,5 x² + 3 x + 5,5 0,5 x² + 2 x + 5,5 − b = 0 / *2 x² + 4 x + 11 − 2 b = 0 Δ = 16 − 4*1*( 11 − 2 b) = 16 − 44 + 8 b = 8 b − 28 = 0 ⇒ b = 3,5 y = x + 3,5 =========== P = 0,5*3,5² = 0,5*12,25 = 6,125

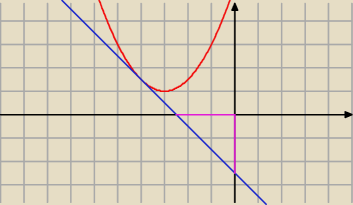
Janek191: 2) y = − x + b y = 0,5 x² + 3 x + 5,5 więc − x + b = 0,5 x² + 3 x + 5,5 / *2 − 2 x + 2 b = x² + 6 x + 11 x² + 8 x + 11 − 2 b = 0 Δ = 64 − 4*1*( 11 − 2b) = 64 − 44 + 8 b = 20 + 8 b = 0 ⇒ b = − 2,5 P = 0,5*2,5² = 0,5*6,25 = 3,125