Ciągi
Domka: Ciąg (Sn) sum częściowych pewnego ciągu (an) określony jest dla każdej liczby naturalnej n≥1
wzorem Sn=(n3−1)(1−p), gdzie p∊R. Wyznacz wszystkie wartości p, dla których ciąg (bn) o
wyrazie ogólnym bn = an − p(n2+1) jest malejący.
Znalazłam wyraz ogólny ciągu (an), odejmując Sn−Sn−1. Później wstawiłam to do podanego wzoru
na (bn), obliczyłam różnicę bn+1−bn i wyszło mi p>6n8n+1. Co mam z tym zrobić?
27 kwi 21:08
Domka: Zastanawia mnie jeszcze kwadratowa postać ciągu bn... Czy to może coś oznaczać?
27 kwi 21:13
Domka: Czy mogę policzyć granicę tego p dla n→∞?
27 kwi 21:32
Mila:
Jeżeli masz kwadratową postać ciągu bn to monotoniczność zmienia się przy przejściu przez xw.
27 kwi 22:29
Domka: Czyli co mam zrobić? Mam postać n2(3−4p)−3n(1−p)+1−2p. Δ chyba jest nieistotna, ważny jest
współczynnik a? Jeśli a>0 to wtedy ciąg b jest malejący do wierzchołka, ale jak obliczyć jego
współrzędną i co ona mi daje?
27 kwi 22:54
Domka: Bo jeśli a=0 to ciąg jest malejący w R, ale nie wiem jak ruszyć tą postać kwadratową.
27 kwi 22:56
Domka: Czy jeśli rośnie a, to xw "ucieka" ?
27 kwi 23:16
Mila:
Czy na pewno taka postać bn?
27 kwi 23:25
Domka: No tak mi wychodzi cały czas. an=(1−p)(3n2−3n+1) ?
27 kwi 23:41
Mila:
Dla bn takie warunki (dla postaci kwadratowej)
a<0 i nw≤1
Wtedy dla n∊N+ będziesz miała funkcję malejącą.
28 kwi 16:35
Domka: nw w Twoim oznaczeniu to?
28 kwi 20:18
Domka: współrzędna wierzchołka?
28 kwi 20:22
Domka: Czy to jest wprowadzone po to, żeby w ciągu zawarła się tylko malejąca połowa paraboli?
28 kwi 20:24
Mila:
nw − współrzędna W.
20:24 tak. I to aby począwszy od n=1 .
Po obliczeniu napisz to narysujemy.
28 kwi 20:27
Domka: Dla postaci liniowej p=0,75, dla kwadratowej z warunku:
a<0 → p>0,75
nw≤1 →p∊(−∞;0,6>∪<0,75;+∞),
czyli p>0,75 a łącznie p≥0,75
28 kwi 20:35
Domka: Dziękuję za pomoc, jak się pomyśli, to to zadanie wcale nie było takie trudne

28 kwi 20:37
Mila:
Przekształcenia okropne. Strasznie udziwnione, mogli ten sam problem inaczej zaprezentować .
Zaraz narysuję dla p=0.8 i zobaczymy jak dla n∊N+ wychodzi.
Tylko cos sobie wydrukuję.
28 kwi 21:42
Mila:
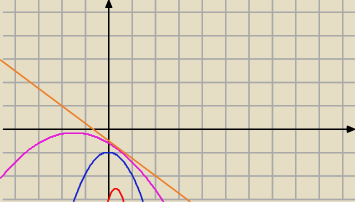
n
2*(3−4*0.8)−3n*(1−0.8)+1−2*0.8
Maleje kwadratowa , ale przelicz jeszcze raz dla kwadratowej.
Czy nie masz odpowiedzi do tego zadania ?
28 kwi 21:54
Domka: Mam odpowiedź i jest to p≥
34 
Wydaje mi się, że dobrze obliczyłam dla postaci kwadratowej...
28 kwi 23:44
Mila:

29 kwi 00:08


 Wydaje mi się, że dobrze obliczyłam dla postaci kwadratowej...
Wydaje mi się, że dobrze obliczyłam dla postaci kwadratowej...
